Момент инерции является одной из важных характеристик, определяющих поведение материала при вращении. Для конструкции, выполненной из двутавра швеллера, знание моментов инерции особенно важно при проектировании и расчете прочности элементов.
Момент инерции двутавра швеллера определяет его способность сопротивляться повороту вокруг оси. Он зависит от формы и размеров сечения двутавра. Чем больше момент инерции, тем труднее вращать элемент, и тем большую нагрузку он может выдержать без деформации.
Для определения момента инерции двутавра швеллера необходимо знать его геометрические параметры, такие как высота и ширина стенок, толщина стенок, радиусы скругления и другие. Поскольку форма двутавра швеллера сложна, точные математические выражения для расчета моментов инерции не всегда могут быть удобны и доступны.
Одним из способов определения моментов инерции двутавра швеллера является использование специальных таблиц или справочников, в которых значения моментов инерции уже рассчитаны и представлены для различных типов и размеров двутавров. Такие таблицы могут быть очень полезными инструментами при проектировании и расчете.
Значение момента инерции
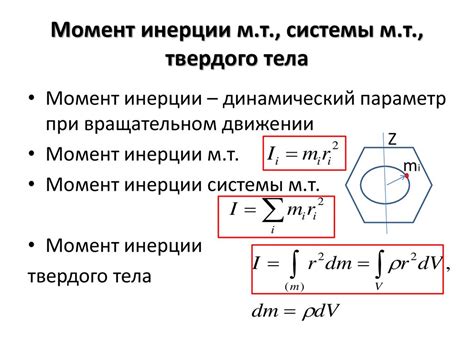
Момент инерции - это физическая величина, характеризующая сопротивление тела изменению его угловой скорости. Зависит от геометрических параметров тела и распределения его массы относительно оси вращения.
Значение момента инерции определяется для каждой оси вращения отдельно. У двутавра швеллера момент инерции зависит от его геометрических параметров, таких как ширина полок, толщина стенок, высота швеллера и т.д.
Момент инерции используется для определения сопротивления тела кручению, а также для решения различных инженерных задач, связанных с расчетами прочности и устойчивости конструкций, в которых используются двутавры швеллера.
Значение момента инерции может быть вычислено аналитически с использованием математических формул, основанных на геометрии профиля швеллера. Также существуют таблицы и руководства, в которых приведены значения моментов инерции для различных типов двутавров швеллера.
Знание момента инерции является важным для проектирования и расчета конструкций с использованием двутавра швеллера. Определение этой физической величины позволяет учитывать его влияние на прочность и устойчивость конструкций, а также предотвращать возможные повреждения и поломки.
Определение момента инерции

Момент инерции является геометрической характеристикой строительного элемента, в данном случае двутавра швеллера, и описывает его сопротивление изменению скорости вращения. Определение момента инерции необходимо для расчета прочностных характеристик конструкции и выбора подходящих стандартных профилей.
Для определения момента инерции двутавра швеллера, необходимо знать его геометрические параметры, такие как ширина полки, высота стенки, толщина полки и стенки, а также длина строительного элемента. Расчет можно произвести как аналитически, используя формулы и таблицы, так и численно, используя специализированные программы.
Зная геометрические параметры двутавра швеллера, можно определить его момент инерции с помощью формулы:
I = (b * h^3 - b1 * h1^3) / 12
где:
- I - момент инерции;
- b - ширина полки;
- h - высота стенки;
- b1 - толщина полки;
- h1 - толщина стенки.
Определенные значения момента инерции позволяют более точно расчитывать прочностные характеристики конструкции и выбирать оптимальный профиль двутавра швеллера для выполнения строительных работ.
Формулы для определения момента инерции
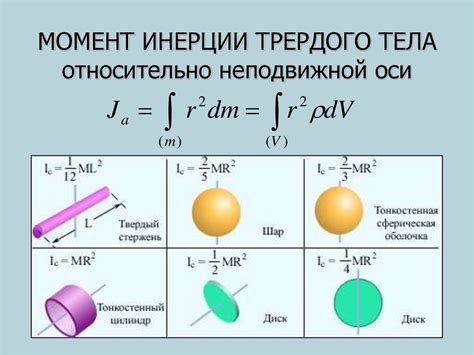
Момент инерции является важным параметром при анализе статической и динамической устойчивости конструкций. Для определения момента инерции двутавра швеллера в первую очередь необходимо знать его геометрические параметры, такие как высота профиля (h), ширина полки (b), толщина полки (t), толщина стенки (s) и радиус закругления (r), если таковой имеется.
Для расчета момента инерции существуют различные формулы в зависимости от формы профиля. Например, для прямоугольного сечения момент инерции может быть вычислен по следующей формуле:
I = (b * (h^3)) / 12
Где I - момент инерции, b - ширина профиля, h - высота профиля. Значение поделено на 12, так как это коэффициент, учитывающий распределение материала в сечении.
Если у двутавра швеллера имеется закругление, то формула становится сложнее и включает в себя также радиус закругления:
I = (b * (h^3) - (b - 2 * r) * (h - 2 * r)^3) / 12
В данной формуле r - радиус закругления. Она учитывает площади закругленных участков, которые считаются отдельно от основного прямоугольного сечения.
Таким образом, зная геометрические параметры двутавра швеллера, можно с легкостью определить его момент инерции,
что позволит проводить анализ различных силовых воздействий на данную конструкцию.
Особенности двутавра швеллера
Двутавр швеллер - это металлический профиль, который имеет форму буквы "H" и используется в строительстве и машиностроении для создания различных конструкций. Особенности этого профиля делают его популярным и широко применяемым в различных отраслях.
Первая особенность двутавра швеллера - его жесткость и прочность. Благодаря форме "H" и специальной конструкции, этот профиль способен выдерживать большие нагрузки и служить в тяжелых условиях. Швеллер обладает высокой степенью статической и динамической прочности, что делает его незаменимым в объектах с высокими требованиями к надежности и безопасности.
Вторая особенность двутавра швеллера - его удобство в монтаже и обработке. Благодаря ровной поверхности и точным размерам, швеллеры легко свариваются и соединяются друг с другом, что упрощает конструкционные работы и сокращает время строительства. Профиль также удобен в обработке - его можно резать, сверлить и гнуть, чтобы создавать различные формы и конфигурации.
Третья особенность двутавра швеллера - его универсальность. Швеллеры могут использоваться для создания самых разнообразных конструкций, начиная от простых рам и стоек, и заканчивая сложными металлическими конструкциями. Они находят применение в строительстве зданий и сооружений, автомобильной промышленности, железнодорожном транспорте и других сферах.
Четвертая особенность двутавра швеллера - его стоимость. Благодаря использованию прочных материалов и эффективной конструкции, швеллеры отличаются высоким соотношением прочности и стоимости. Это делает их более экономически выгодным выбором по сравнению с другими металлическими профилями.
В заключение, двутавр швеллер - это особый металлический профиль, который обладает рядом преимуществ. Его жесткость, удобство в монтаже, универсальность и привлекательная стоимость делают его широко применяемым и популярным в различных отраслях.
Расчет момента инерции двутавра швеллера

Момент инерции - это важная характеристика фигуры, указывающая на ее способность сопротивляться вращению вокруг оси. Расчет момента инерции для двутавра швеллера является неотъемлемой частью проектирования и строительства.
Для расчета момента инерции двутавра швеллера необходимо знать его размеры и параметры. Геометрические размеры включают высоту поперечного сечения, ширину верхней и нижней полки, толщину стенки и радиус закругления углов.
Момент инерции двутавра швеллера можно найти с помощью специальных формул и таблиц. Одна из таких формул представляет момент инерции как сумму моментов инерции полок и стенок двутавра. Эта формула позволяет получить точные значения момента инерции.
Расчет момента инерции двутавра швеллера позволяет оценить его жесткость, прочность и способность сопротивляться деформации под действием нагрузки. Чем больше момент инерции, тем лучше сопротивление стального профиля вращению и изгибу.
Таким образом, расчет момента инерции двутавра швеллера является неотъемлемым шагом в процессе проектирования и выбора нужного профиля для конкретной конструкции.
Пример расчета момента инерции швеллера
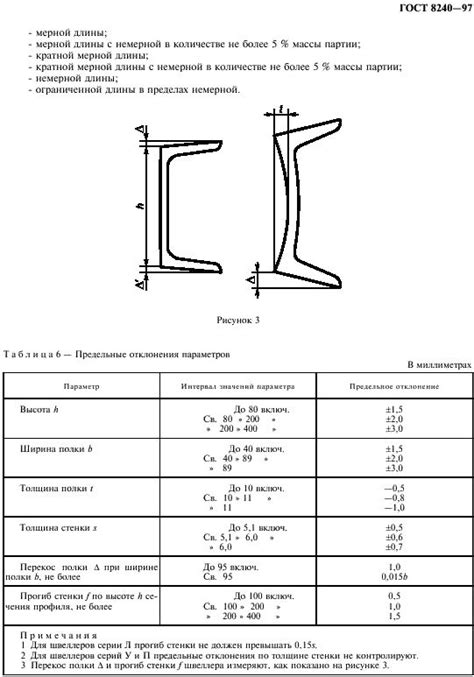
Для определения момента инерции двутавра швеллера необходимо рассчитать его геометрические характеристики и учесть особенности его конструкции. Рассмотрим пример расчета момента инерции швеллера.
Пусть у нас имеется двутавр швеллера с такими параметрами: ширина полки b = 120 мм, высота полки h = 220 мм, толщина стенки полки t = 5 мм, толщина горизонтальной панели полки t1 = 8 мм, и расстояние от центра тяжести до верхней кромки полки c = 100 мм.
Для определения момента инерции швеллера необходимо воспользоваться следующей формулой:
I = (b * h^3 - (b - 2 * t) * (h - 2 * t)^3) / 12
В нашем случае:
- Ширина полки b = 120 мм
- Высота полки h = 220 мм
- Толщина стенки полки t = 5 мм
- Толщина горизонтальной панели полки t1 = 8 мм
- Расстояние от центра тяжести до верхней кромки полки c = 100 мм
Подставим эти значения в формулу:
| I = (120 * 220^3 - (120 - 2 * 5) * (220 - 2 * 8)^3) / 12 |
Получим момент инерции швеллера по данной формуле. Значение будет зависеть от параметров швеллера и позволит оценить его жесткость и способность противостоять изгибающим нагрузкам.
Выводы

Определение моментов инерции двутавра швеллера является важной задачей в инженерной практике. Знание моментов инерции позволяет рассчитывать прочностные характеристики конструкций, определять их устойчивость и предсказывать поведение при различных нагрузках.
Для определения момента инерции двутавра швеллера используются различные методы. Один из наиболее распространенных методов - метод геометрического пути, основанный на знании геометрических параметров профиля. При этом профиль двутавра швеллера аппроксимируется составной фигурой, состоящей из прямоугольников и круговых сегментов, и вычисляется момент инерции относительно выбранных осей.
Моменты инерции двутавра швеллера имеют важное значение при проектировании различных конструкций, таких как колонны, балки, фермы. Они позволяют рассчитывать напряжения и деформации, определять границы применимости материала, а также оценивать устойчивость и жесткость конструкций.
Определение моментов инерции двутавра швеллера требует точной геометрической информации о профиле. Поэтому перед проведением измерений и расчетов необходимо убедиться в правильности и достоверности геометрических данных, а также учесть возможные погрешности, возникающие при изготовлении и монтаже конструкций.
Использование компьютерных программ и специальных технологий позволяет автоматизировать процесс определения моментов инерции двутавра швеллера, что упрощает и ускоряет процесс проектирования и анализа конструкций. Это особенно важно в случае сложных и больших по объему проектов, где расчеты требуют значительных ресурсов и времени.
Вопрос-ответ

Как определить моменты инерции двутавра швеллера?
Для определения моментов инерции двутавра швеллера необходимо знать его геометрические характеристики, такие как ширина полки, высота полки, толщина стенки и расстояние от центра масс до осей полок. Зная эти параметры, можно воспользоваться стандартными формулами для расчета моментов инерции двутавра.
Какие геометрические параметры нужны для определения моментов инерции двутавра швеллера?
Для определения моментов инерции двутавра швеллера необходимо знать ширину полки, высоту полки, толщину стенки и расстояние от центра масс до осей полок.
Какие формулы используются для расчета моментов инерции двутавра швеллера?
Для расчета моментов инерции двутавра швеллера используются стандартные формулы, которые зависят от его геометрических параметров. Например, для расчета момента инерции относительно оси, проходящей через центр масс и перпендикулярной плоскости двутавра, используется формула I = (b * h^3 - (b - t)^3 * (h - 2 * t)^3) / 12, где b - ширина полки, h - высота полки, t - толщина стенки.
Можно ли рассчитать моменты инерции двутавра швеллера без знания его геометрических характеристик?
Нет, невозможно рассчитать моменты инерции двутавра швеллера без знания его геометрических характеристик. Геометрические параметры, такие как ширина полки, высота полки, толщина стенки и расстояние от центра масс до осей полок, являются основными параметрами, от которых зависят моменты инерции.
Есть ли таблицы, в которых приведены моменты инерции двутавров швеллера для разных размеров?
Да, существуют таблицы, в которых приведены значения моментов инерции двутавров швеллера для разных размеров. В этих таблицах указываются геометрические параметры двутавра и соответствующие им моменты инерции. Такие таблицы можно найти в специализированной литературе по конструкционным материалам и инженерным расчетам.
