Dash Minecraft - это популярная игра про строительство и выживание в открытом мире, в которой игроки могут создавать различные объекты и конструкции с помощью геометрических фигур. Эти геометрии обладают уникальными идентификаторами, которые позволяют игрокам легко находить и использовать их в игре.
Список геометрий Dash Minecraft с идентификатором включает в себя различные формы и фигуры, такие как куб, сфера, цилиндр и многое другое. Каждая геометрия имеет свои уникальные параметры, такие как размер, материал и текстура, которые можно настраивать в зависимости от потребностей игрока.
Использование геометрий Dash Minecraft с идентификатором позволяет игрокам быстро и легко создавать сложные и интересные объекты в игре. Они также помогают улучшить визуальное представление мира игры, делая его более реалистичным и привлекательным.
Выпуклая элипсоидная геометрия

Выпуклая элипсоидная геометрия является одной из форм геометрии в Minecraft Dash. Это форма, которая представляет собой трехмерный объект в форме овала или эллипсоида. Она отличается от других форм своим выпуклым изгибом, т.е. не имеет вогнутых частей.
Выпуклая элипсоидная геометрия может использоваться для создания различных объектов и структур в Minecraft Dash. Например, с ее помощью можно создать куполообразные строения, полусферы, скульптуры и многое другое.
Для создания выпуклой элипсоидной геометрии в Minecraft Dash доступны различные команды и программы. Некоторые из них позволяют автоматически генерировать элипсоиды заданных размеров и параметров. Например, команда "элипсоид" может использоваться для создания выпуклого элипсоида по заданным координатам, радиусам и текстурам.
При создании выпуклой элипсоидной геометрии важно учитывать ее размеры и пропорции. Также следует учитывать материал, который будет использован для построения геометрии. Некоторые материалы могут быть более подходящими для создания эффектов света и тени, а также для обеспечения прочности и стабильности структуры.
Выпуклая элипсоидная геометрия может быть использована как самостоятельный объект, так и в качестве части более сложной конструкции или декоративного элемента. Важно помнить, что форма выпуклой элипсоидной геометрии может быть изменена путем добавления или удаления блоков, что позволяет создавать уникальные и интересные структуры.
В результате мы можем видеть, что выпуклая элипсоидная геометрия является важным элементом для создания различных объектов и структур в Minecraft Dash. Она предоставляет возможности для творчества и экспериментирования с формой и пропорциями, что делает игру еще более увлекательной.
Многогранная геометрия с отверстием
Многогранная геометрия – это раздел геометрии, изучающий многогранные фигуры, то есть фигуры, ограниченные плоскими многоугольниками (гранями). Однако, в некоторых случаях, многогранные фигуры могут иметь отверстия или полости. Такая многогранная геометрия с отверстием является интересной и имеет свои особенности.
Многогранная геометрия с отверстием может быть представлена различными формами и конфигурациями. Одним из примеров таких фигур является многогранник с отверстием в виде цилиндрического туннеля. Этот многогранник имеет две основания, которые образуют плоские многоугольники, и боковую поверхность, которая представляет собой цилиндрическую оболочку. Внутри этой оболочки находится полость - туннель.
Одной из особенностей многогранной геометрии с отверстием является наличие дополнительной поверхности - внешней и внутренней. Внешняя поверхность представляет собой оболочку фигуры, ограниченной гранями, включая отверстия и полости. Внутренняя поверхность находится внутри фигуры и является поверхностью, ограничивающей полость. В то время как внешняя поверхность имеет различные грани и углы, внутренняя поверхность, как правило, является плоской.
Многогранная геометрия с отверстием может использоваться в различных областях, таких как архитектура, дизайн и инженерия. Например, многогранник с отверстием может использоваться для создания моделей зданий с привлекательными и сложными формами. Также многогранная геометрия с отверстием может быть использована для создания моделей в медицине или визуализации данных.
Примеры многогранной геометрии с отверстием:
- Многогранник с отверстием в виде цилиндрического туннеля.
- Многогранная фигура с отверстием в виде сферической полости.
- Многогранник с отверстием в виде призматического коридора.
- Многогранная фигура с отверстием в виде торуса.
Заключение:
Многогранная геометрия с отверстием – это интересный раздел геометрии, изучающий многогранные фигуры с наличием отверстий и полостей. Такие фигуры могут иметь сложные формы и находить применение в архитектуре, дизайне и инженерии.
Плоская геометрия с закругленными углами
Плоская геометрия с закругленными углами является одной из разновидностей геометрии, которая используется в различных областях, таких как дизайн, архитектура и компьютерная графика. Она отличается от классической геометрии тем, что ее фигуры имеют не только прямые углы, но и закругленные края и углы.
Преимущества использования плоской геометрии с закругленными углами включают:
- Эстетический вид: Закругленные углы придают фигурам мягкий и приятный внешний вид, делая их более привлекательными и современными.
- Безопасность: Закругленные углы уменьшают риск получения травмы при контакте с фигурами. Они могут быть особенно полезны в местах, где дети часто находятся, таких как детские площадки или школьные кабинеты.
- Удобство: Фигуры с закругленными углами могут быть проще в использовании и более удобными для обработки, поскольку отсутствие острых краев делает их менее подверженными повреждениям или износу.
Важно отметить, что в плоской геометрии с закругленными углами есть несколько основных фигур:
| Фигура | Описание |
|---|---|
| Круг | Фигура, в которой все точки находятся на одинаковом расстоянии от центра. Она имеет только закругленные углы и края. |
| Эллипс | Фигура, в которой сумма расстояний от любой точки на периферии до двух фокусов равна постоянной величине. Она также имеет закругленные углы и края. |
| Многоугольник | Фигура, которая имеет более двух прямых углов и может иметь один или более закругленных углов. |
| Ромб | Многоугольник, у которого все стороны равны. У него также могут быть закругленные углы. |
Плоская геометрия с закругленными углами широко используется в современном дизайне интерфейсов, таких как веб-сайты и мобильные приложения. Она помогает создавать современный, привлекательный и удобный пользовательский интерфейс, который приятно воспринимается глазом и подходит для использования на различных устройствах и экранах.
Несимметричная геометрия призмы
Призма - это геометрическое тело, которое состоит из двух параллельных многоугольников (оснований), соединенных прямыми отрезками (гранями). Но что делает призму несимметричной?
Несимметричная геометрия призмы означает, что все ее грани не являются равными и подобными. В сравнении с симметричной призмой, несимметричная призма имеет разные размеры граней, различные углы у оснований и грани и неравные диагонали.
Несимметричная геометрия призмы может создавать уникальные эффекты и визуальные интересы в архитектуре и дизайне. Это может быть использовано для создания современных и оригинальных строений, которые привлекают внимание и выделяются среди других конструкций.
Примером несимметричной призмы может быть строение с асимметричной крышей или стенами, которые имеют разные градиенты или формы. Такие призмы могут быть использованы в зданиях, мебели, светильниках и других предметах интерьера и экстерьера.
Несимметричная геометрия призмы требует более сложных вычислений и проектирования, поскольку каждая грань может иметь разные параметры и формы. Однако, такие призмы могут создавать удивительные и уникальные эффекты, которые невозможно достичь симметричными формами.
Сферическая геометрия с вершинами
Сферическая геометрия – это раздел геометрии, который изучает пространство на сфере. Она является одним из типов неевклидовой геометрии, отличающейся от классической евклидовой геометрии.
Сферическая геометрия с вершинами – это особый вид сферической геометрии, который изучает многогранники, вершины которых лежат на поверхности сферы.
В такой геометрии можно рассмотреть различные геометрические фигуры, но особое внимание уделяется многогранникам. Многогранники в сферической геометрии имеют форму замкнутых поверхностей, состоящих из ребер и граней.
Важной характеристикой многогранников в сферической геометрии является количество вершин. Каждый многогранник имеет определенное число вершин, которое зависит от его формы. Например, тетраэдр – многогранник с четырьмя вершинами, а икосаэдр – многогранник с двенадцатью вершинами.
Сферическая геометрия с вершинами имеет широкое применение в различных областях, включая астрономию, геодезию, картографию и компьютерную графику. Она позволяет адаптировать пространственные модели и различные геометрические задачи к сферической форме Земли или других небесных тел.
Примеры многогранников в сферической геометрии с вершинами:
- Тетраэдр (четырехугольник)
- Гексаэдр (шестиугольник)
- Октаэдр (восьмиугольник)
- Додекаэдр (двенадцатиугольник)
- Икосаэдр (двадцатиугольник)
Сферическая геометрия с вершинами представляет собой интересное и необычное исследовательское направление. Ее применение в реальных задачах позволяет получить более точные и удобочитаемые модели пространства.
Торообразная геометрия с отмеченными гранями
Торообразная геометрия является одним из видов геометрии, которая имеет форму тора, напоминающую кольцевой донатс. В этой геометрии можно выделить несколько отмеченных граней, которые играют особую роль.
Отмеченные грани в торообразной геометрии обычно выделены цветом или текстурой для того, чтобы их можно было проще различить и использовать внутри игры. Они часто представлены в виде плоскостей или поверхностей, которые можно динамически изменять, вращать и взаимодействовать с ними.
Вот некоторые из типичных отмеченных граней, которые могут встречаться в торообразной геометрии:
- Внешняя грань - это наружная поверхность тора, которая может быть окрашена в особый цвет или иметь свою уникальную текстуру.
- Внутренняя грань - это внутренняя поверхность тора, которая также может быть окрашена или иметь специальную текстуру.
- Горизонтальные грани - это горизонтальные сегменты тора, которые можно использовать для создания платформ или других структур.
- Вертикальные грани - это вертикальные сегменты тора, которые могут служить опорами или стенами.
- Внутренние грани - это сегменты внутренней поверхности тора, которые можно использовать для создания тайных проходов или пещер.
Использование отмеченных граней в торообразной геометрии может значительно расширить возможности игрового процесса и позволить игрокам создавать более сложные и интересные структуры в Minecraft.
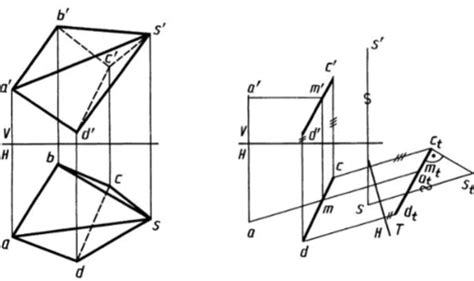
Гиперболическая геометрия с вырезанными краями
Гиперболическая геометрия с вырезанными краями (также известная как гиперболическая геометрия без границ) является одной из разновидностей гиперболической геометрии. Она содержит много общих свойств с обычной гиперболической геометрией, но имеет также ряд интересных особенностей, вызванных наличием вырезанных краев.
В гиперболической геометрии с вырезанными краями пространство плоскости делится на гиперболические треугольники, похожие на обычные треугольники, но с некоторыми отличиями. Гиперболические треугольники имеют углы, сумма которых всегда меньше 180 градусов. Это является проявлением гиперболической кривизны пространства плоскости.
Особенностью гиперболической геометрии без границ являются вырезанные края. В этом случае, геометрические объекты, находящиеся рядом с краями, имеют некоторые особенности. Например, гиперболическое пространство без границ может содержать цепочку бесконечно уменьшающихся треугольников, которые представляются как многоугольники с бесконечным числом углов. Это вызывает некоторые интересные математические исследования, связанные с гиперболической геометрией с вырезанными краями.
Гиперболическая геометрия с вырезанными краями находит применение в различных областях, включая математику, физику и компьютерные науки. Она используется для моделирования сложных структур и пространственных отношений, а также для анализа и визуализации данных. Гиперболические геометрии с вырезанными краями также активно применяются в игровой индустрии, в том числе в игре Dash Minecraft.
Четырехмерная геометрия с перемычками

Четырехмерная геометрия с перемычками является одной из наиболее интересных и сложных областей математики. Она изучает пространства и объекты, которые имеют четыре измерения. В таких пространствах, перемещение возможно не только вперед-назад, влево-вправо и вверх-вниз, как в трехмерном пространстве, но и в четвертом измерении - которое невозможно представить геометрически.
Одним из основных объектов в четырехмерной геометрии с перемычками является тессеракт. Тессеракт - это четырехмерный аналог куба или трехмерного куба. Он состоит из 8-ми вершин, 24-ех ребер, 32-ух граней и 16-и клеток. Также существуют и другие четырехмерные геометрические объекты, такие как пентакордел, гекадекакордел и др.
Четырехмерная геометрия с перемычками имеет множество применений в различных областях науки и инженерии. Она используется в компьютерной графике и визуализации данных, в освещении и моделировании трехмерных объектов, а также в анализе и синтезе сигналов.
В связи с сложностью и абстрактностью четырехмерной геометрии с перемычками, в ее изучении применяются различные методы и инструменты, такие как компьютерные моделирование, математическая формализация, графические представления и другие. Несмотря на свои сложности, четырехмерная геометрия с перемычками предоставляет новые возможности для исследования и понимания пространства и структуры объектов в четвертом измерении.




