Уравнение потенциалов металлов является одним из базовых понятий в области материаловедения и электрохимии. Это уравнение позволяет определить потенциал электродов из различных металлов, находящихся в электролите, и предоставляет инструмент для изучения электрохимических процессов, происходящих в металлах.
Основная идея уравнения заключается в том, что каждый металл имеет свой химический потенциал или электрохимический потенциал, который можно измерить. При наличии разной концентрации ионов металла в электролите, происходит перенос электронов через границу раздела между металлом и электролитом, что приводит к возникновению разности потенциалов.
Применение уравнения потенциалов металлов в широком смысле простирается на множество областей науки и техники. В частности, данное уравнение используется в электрохимическом анализе, электрохимическом осаждении пленок, коррозии металлов, а также в создании электродных материалов с заданными свойствами.
Исследование уравнения потенциалов металлов позволяет более глубоко понять основные принципы процессов, происходящих внутри металла при контакте с электролитом. Это знание не только интересно с научной точки зрения, но также имеет практическое применение в различных областях, таких как материаловедение, каталитическая химия и электротехника.
Уравнение потенциалов металлов
Уравнение потенциалов металлов - это основной инструмент в физике и химии металлов для описания и предсказания их свойств. Оно является математической моделью, которая основывается на принципе минимума свободной энергии и позволяет определить максимально стабильное состояние металла.
Уравнение потенциалов металлов используется для решения широкого спектра задач, связанных с металлургией, электрохимией, нанотехнологиями и другими областями. Оно позволяет предсказывать свойства металлов в различных условиях, таких как температура, давление и состав окружающей среды. Также с помощью уравнения можно определить электрохимический потенциал металла и его взаимодействие с другими веществами.
В основе уравнения потенциалов металлов лежит принцип электронейтральности и равновесия электрохимических реакций. Математически оно выражается через сумму потенциалов каждого иона металла и потенциалов окружающих реагентов. Используя эту модель, можно определить электрохимические потенциалы различных пассивных и активных металлов и их сплавов, а также предсказать их коррозионную стойкость и реакционную способность.
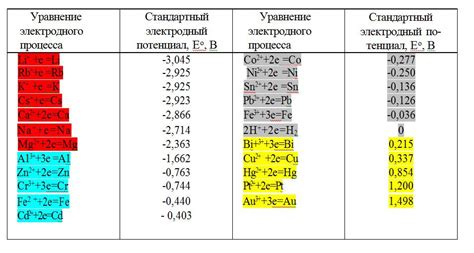
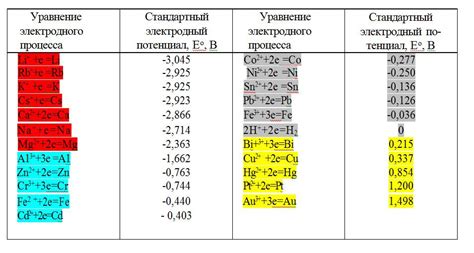
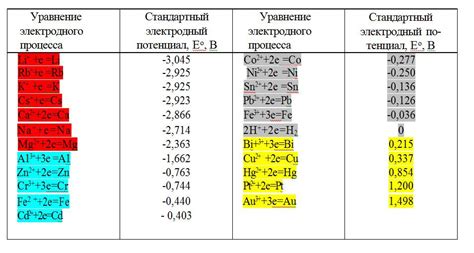
В таблице потенциалов металлов приведены значения потенциалов различных металлов относительно стандартного водородного электрода. По этим значениям можно сравнивать потенциалы металлов и предсказывать их способность к окислительно-восстановительным реакциям. Например, металлы с более положительными потенциалами обладают большей способностью к окислительным реакциям, а с более отрицательными - к восстановительным. Такие сравнения и прогнозы являются важными при выборе материалов для различных технических и химических приложений.
Основные понятия
Уравнение потенциалов металлов - это математическое выражение, которое описывает распределение потенциала внутри металлического образца.
Потенциал - это величина, характеризующая энергию единичного электрического заряда в данной точке пространства. В металлах потенциал является константой и равен нулю на поверхности образца.
Уравнение потенциалов металлов состоит из дифференциального уравнения - уравнения Лапласа, и граничных условий, которые определяют потенциалы на границах металлического образца.
Решение уравнения потенциалов металлов позволяет определить потенциалы внутри образца и, следовательно, понять распределение электрического поля и электростатических свойств металла.
Уравнение потенциалов металлов находит применение в различных областях науки и техники, таких как физика металлов, электрохимия, электрические изоляторы, полупроводники и другие.
Металлы и электрохимический потенциал
Металлы являются одними из наиболее распространенных материалов, которые активно применяются в различных отраслях промышленности и научных исследований. Характерной особенностью металлов является их способность к проводимости электричества. Это свойство связано с наличием свободных электронов в зоне проводимости, которые могут легко перемещаться по структуре металла.
Электрохимический потенциал является одним из основных параметров, характеризующих поведение металлов в различных окружающих средах. Этот потенциал можно определить как разность потенциалов между металлом и некоторым эталонным электродом, который является системой с известным потенциалом. Измерение электрохимического потенциала металла позволяет понять его активность в электрохимических процессах, а также его вероятность реагировать с окружающей средой.
Электрохимический потенциал металла является важным параметром при выборе материалов для конкретных технических задач. Он может указывать на степень коррозионной стойкости металла, его способность к взаимодействию с другими материалами, а также на возможность использования металла в различных агрессивных средах. Знание электрохимического потенциала металла позволяет эффективно проектировать и разрабатывать новые материалы, а также проводить исследования с целью определения их свойств и возможностей применения в различных сферах науки и промышленности.
Уравнение потенциалов металлов и его компоненты
Уравнение потенциалов металлов, также известное как уравнение Ферми-Дирака, является одним из основных уравнений в физике металлов. Оно описывает распределение электронов в энергетических уровнях металла при равновесном состоянии.
Уравнение потенциалов металлов можно представить в виде суммы компонент. Первая компонента отвечает за энергетическую часть уравнения и зависит от всех энергетических уровней электронов в металле. Вторая компонента учитывает взаимодействие электронов между собой и с ионами металла.
Основная компонента уравнения потенциалов металлов, называемая электронной частью, определяет распределение фермиевской функции, которая описывает вероятность нахождения электрона в определенном энергетическом состоянии. Данная компонента зависит от химического потенциала металла, температуры системы и других показателей.
Вторая компонента уравнения потенциалов металлов, называемая ионной частью, учитывает экранировку электрического поля ионами металла. Она определяет поляризацию ионов, что имеет важное значение для определения энергетического состояния металла и его поведения во внешнем электрическом поле.
Уравнение потенциалов металлов находит широкое применение в различных областях науки и техники, таких как физика полупроводников, квантовая механика и электроника. Оно позволяет более точно описывать электронные свойства металлов, а также предсказывать их поведение в разных условиях.
Применение уравнения потенциалов металлов в научной и практической сферах
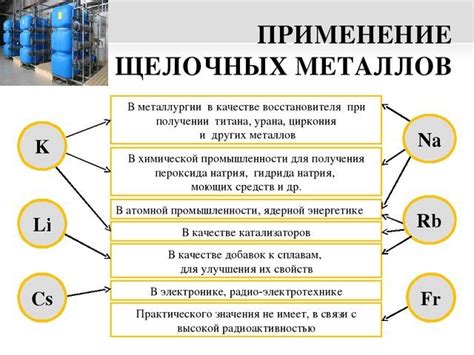
Уравнение потенциалов металлов – это фундаментальный закон, который находит широкое применение в научных и практических областях. Оно позволяет описывать и предсказывать электрохимические процессы, происходящие в металлических материалах.
В научной сфере уравнение потенциалов металлов используется для исследования электрохимических реакций, которые происходят при взаимодействии металлических материалов с окружающей средой. Оно является основой для разработки теоретических моделей, которые позволяют выявить причины различных физико-химических явлений.
Применение уравнения потенциалов металлов также находит важное применение в практических сферах, таких как материаловедение и электрохимия. С его помощью можно определить коррозийные свойства металлических материалов и разработать способы их защиты от коррозии. Также уравнение потенциалов металлов позволяет управлять и контролировать электрохимические процессы, например, при электрохимическом осаждении металла на поверхности.
Другой областью, где находит применение уравнение потенциалов металлов, является электрохимическая энергетика. Оно используется при проектировании и разработке электролитических и гальванических элементов, таких как аккумуляторы и батареи. Опираясь на уравнение потенциалов металлов, можно оптимизировать работу электрохимических систем и повысить их эффективность.
В заключение следует отметить, что уравнение потенциалов металлов является основой для понимания и изучения физико-химических процессов, происходящих в металлических материалах. Его применение в научных и практических областях позволяет не только углубить наши знания о свойствах металлов, но и создать новые материалы и технологии, которые применяются в различных сферах человеческой деятельности.
Вопрос-ответ

Что такое уравнение потенциалов металлов?
Уравнение потенциалов металлов - это математическое уравнение, которое описывает равновесие потенциалов в металлическом проводнике. Оно позволяет определить распределение электрического потенциала внутри металла при заданных условиях.
Какие основные понятия связаны с уравнением потенциалов металлов?
Основные понятия, связанные с уравнением потенциалов металлов, включают электрический потенциал, электрическое поле, заряд, проводимость, равновесие и граничные условия. Эти понятия являются ключевыми для понимания и применения уравнения в различных задачах.
Каковы применения уравнения потенциалов металлов?
Уравнение потенциалов металлов находит широкое применение в различных областях, таких как электростатика, электродинамика, электроника и теоретическая физика. Оно позволяет моделировать и анализировать электрические свойства металлических проводников, предсказывать их поведение при воздействии внешних полей и разрабатывать новые устройства и технологии.
Какие граничные условия нужно задавать при решении уравнения потенциалов металлов?
Граничные условия, которые нужно задавать при решении уравнения потенциалов металлов, зависят от конкретной задачи. Например, в случае равномерно заряженной сферы, граничное условие может быть задано в виде равенства потенциалов на поверхности и бесконечности. В других случаях могут использоваться различные комбинации граничных условий, например, задание зарядов на поверхностях и ограничений на электрическое поле.
Какие методы существуют для решения уравнения потенциалов металлов?
Для решения уравнения потенциалов металлов существует несколько методов. Одним из наиболее распространенных является метод разделения переменных, при котором уравнение разбивается на несколько простых уравнений, решение которых находится последовательно. Другим методом является метод конечных элементов, который позволяет численно решать уравнение с использованием дискретного приближения. Кроме того, существуют и другие методы, такие как методы Фурье, интегральные уравнения и методы решения дифференциальных уравнений.
