Вычисление объема металла по способу Архимеда является одним из важных этапов при проведении физических экспериментов и исследований в области металлургии и материаловедения. Для этого необходимо найти множитель, который позволяет определить объем металлического образца на основе различных измерений и данных.
Алгоритм нахождения множителя для вычисления объема металла по способу Архимеда начинается с определения плотности материала. Для этого необходимо взять металлический образец и измерить его массу с помощью весов. Затем измеряется объем воды, в которую погружается образец. Этот объем можно измерить с помощью штатной мерной колбы или другого прибора для измерения объема.
Далее происходит сравнение плотности металла с плотностью воды. Если плотность металла больше плотности воды, то он будет тонуть в воде и вытеснять определенный объем жидкости. Если плотность металла меньше плотности воды, то он будет всплывать и не вытеснять воду. Коэффициент, на который необходимо умножить разницу объемов воды до и после погружения металла, и определяет искомый объем металла.
Таким образом, алгоритм нахождения множителя для вычисления объема металла по способу Архимеда основан на сравнении плотности металла с плотностью воды и вычислении разницы объемов воды до и после погружения образца. Этот метод позволяет получить достоверные результаты при определении объема металла и является важным инструментом для металлургов и материаловедов.
Алгоритм нахождения множителя

Для вычисления объема металла по способу Архимеда необходимо использовать определенный множитель. От выбора правильного множителя зависит точность результатов и последующих расчетов. В данной теме рассмотрим алгоритм нахождения множителя.
Первым шагом в алгоритме нахождения множителя является измерение объема погруженной в жидкость детали. Для этого необходимо погрузить деталь в известную жидкость и измерить объем, который занимает жидкость до и после погружения детали. Разность объемов позволит нам найти объем детали.
Вторым шагом является измерение плотности жидкости, в которую погружается деталь. Для этого можно использовать плотнометр или другие приборы. Измеренное значение плотности позволит нам правильно рассчитать множитель.
Третий шаг состоит в использовании формулы для вычисления множителя. Формула имеет вид: множитель = плотность жидкости / плотность материала детали. Результатом будет числовое значение множителя, которое можно использовать при последующих расчетах.
Важно отметить, что точность вычислений зависит от точности измерений и выбора правильной формулы. При работе с металлом, также необходимо учитывать его состав и возможные примеси, которые могут влиять на результаты. Поэтому рекомендуется применять алгоритм нахождения множителя в сочетании с другими методами контроля и измерений, чтобы получить максимально точные результаты.
Вычисление объема металла
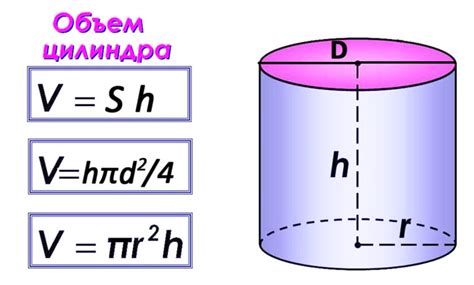
Вычисление объема металла - это процесс определения объема материала, из которого изготовлен объект. Одним из способов вычисления объема металла является метод Архимеда, основанный на принципе плавучести.
Согласно принципу Архимеда, подводимый к полной погруженности в жидкость объект (например, металлический предмет) выталкивает из этой жидкости объем жидкости, равный своему объему. Данный принцип позволяет определить объем металла, используя измерения массы погруженного предмета и плотности жидкости, в которую он погружен.
Для вычисления объема металла по методу Архимеда необходимо выполнить следующие шаги:
- Измерить массу металлического предмета. Это может быть сделано, например, с помощью весов.
- Определить плотность жидкости. Плотность может быть известна из предыдущих измерений или исследований.
- Погрузить металлический предмет в жидкость.
- Измерить объем погруженной жидкости. Для этого необходимо измерить изменение уровня жидкости или использовать специальное устройство для измерения объема.
После выполнения этих шагов можно приступить к вычислению объема металла по формуле, основанной на принципе Архимеда:
Объем металла = объем погруженной жидкости = масса металла / плотность жидкости.
Таким образом, вычисление объема металла по методу Архимеда позволяет определить величину объема материала, что имеет широкое применение в инженерии, строительстве и других отраслях, где необходимо контролировать объем и массу материалов.
Способ Архимеда

Способ Архимеда является одним из методов для определения объема тела, основанным на принципе Архимеда. Этот способ позволяет точно измерить объем металла, используя его плавучесть в жидкости.
Для применения способа Архимеда необходимо иметь две известные величины - массу металла и плотность жидкости, в которую он погружается. На основе этих данных можно определить объем металла.
Применение данного способа особенно полезно при определении объема сложных геометрических форм, так как в этом случае использование стандартных методов объемного измерения может быть затруднительным.
Правило Архимеда позволяет сделать вывод о том, что при погружении тела в жидкость оно будет испытывать силу Архимеда, равную весу вытесненной жидкости. Исходя из этого, можно рассчитать объем тела, зная плотность жидкости и изменение силы Архимеда при погружении тела в нее.
В итоге, способ Архимеда позволяет достаточно точно определить объем металла по его плавучести в жидкости. Этот метод широко применяется в научных и инженерных расчетах, а также в промышленности для измерения объемов различных материалов.
Преимущества алгоритма нахождения множителя для вычисления объема металла по способу Архимеда
Алгоритм нахождения множителя для вычисления объема металла по способу Архимеда обладает рядом преимуществ, которые делают его эффективным и удобным инструментом для проведения таких вычислений.
1. Простота и доступность: Данный алгоритм основан на физических принципах и не требует сложных математических выкладок. Поэтому его использование может быть доступно даже для людей без специальной математической подготовки.
2. Надежность и точность: Данный алгоритм основывается на принципе Архимеда, который предусматривает, что плавающее тело выталкивает из себя объем жидкости, равный своему объему. Это гарантирует точность и надежность результатов вычислений.
3. Возможность использования для различных материалов: Алгоритм нахождения множителя может быть применен для вычисления объема металла любой формы и размера, не зависимо от его плотности и химического состава.
4. Возможность массовых вычислений: Данный алгоритм позволяет проводить вычисления объема металла для большого количества образцов одновременно. Это существенно экономит время и упрощает работу в условиях, когда требуется обработать большой массив данных.
В итоге, алгоритм нахождения множителя для вычисления объема металла по способу Архимеда является простым, надежным и универсальным инструментом, который позволяет проводить вычисления объема металла с высокой точностью и эффективностью. Он может быть полезен в различных областях, связанных с измерением объема и плотности материалов, и является отличной альтернативой более сложным и затратным методам вычислений.
Точность вычислений

При вычислении объема металла по способу Архимеда, точность является ключевым фактором. Чем точнее будут выполнены вычисления, тем более точный результат мы получим. Поэтому необходимо уделить особое внимание выбору алгоритма и методики решения задачи.
Одним из факторов, влияющих на точность вычислений, является выбор единиц измерения. Важно использовать подходящую систему измерений, чтобы избежать ошибок округления и учета производных единиц. Кроме того, необходимо учитывать исходные данные с необходимой точностью, чтобы исключить накопление ошибок погрешности.
Еще одним аспектом, влияющим на точность вычислений, является оценка погрешности метода. Необходимо проводить анализ возможных погрешностей и поиска пути их устранения. Кроме того, необходимо проверить стабильность алгоритма и его способность к справлению с численными нестабильностями.
- Одним из методов повышения точности вычислений может быть использование многократного повторения алгоритма с различными параметрами и усреднением результатов.
- Также можно использовать метод Монте-Карло для оценки погрешности и проведения статистической оценки значений.
- Для более точного учета особенностей геометрии объекта можно разбить его на более мелкие части и провести вычисления для каждой из них, а затем сложить результаты.
Точность вычислений имеет прямое влияние на достоверность и полезность полученных результатов. Поэтому рекомендуется уделить должное внимание этому аспекту при разработке и реализации алгоритма нахождения множителя для вычисления объема металла по способу Архимеда.
Универсальность алгоритма

Алгоритм нахождения множителя для вычисления объема металла по способу Архимеда является достаточно универсальным, так как может быть применен в широком спектре задач, связанных с определением объема различных материалов.
Этот алгоритм позволяет определить объем металла с высокой точностью, основываясь на основных принципах архимедовой силы, которая действует на тело, погруженное в жидкость. Метод заключается в том, чтобы измерить разницу давлений на дне жидкости с и без погруженного металлического образца.
Данная процедура основывается на простых законах физики и может быть применена для любого материала, с особым применением в отраслях, связанных с металлургией, инженерией и промышленностью.
Использование данного алгоритма позволяет эффективно решать задачи, связанные с нахождением объема, что позволяет оптимизировать процессы производства, контроля качества и так далее. Кроме того, универсальность алгоритма позволяет его применение в широком спектре научных исследований, связанных с определением физических свойств различных материалов.
Практическое применение

Алгоритм нахождения множителя для вычисления объема металла по способу Архимеда имеет широкое практическое применение в различных отраслях. Особенно важным он является в металлургической промышленности, где точное определение объема металла необходимо для процессов обработки и манипуляции с материалами.
Например, алгоритм может использоваться при расчете объема металлических заготовок или изделий перед их обработкой. Это позволяет точно определить необходимое количество сырья и провести эффективное планирование производственных процессов.
Также алгоритм может применяться при контроле качества металлических изделий. Путем сравнения объема металла до и после обработки можно выявить возможные дефекты или повреждения в изделии. Это позволяет раннее обнаружить проблемы и предпринять меры по их устранению.
Кроме того, алгоритм может быть полезен при проведении исследований и экспериментов, связанных с физическими свойствами металлов. Поскольку объем металла является одним из основных параметров, на него может влиять ряд факторов, таких как температура, давление и состав среды. Алгоритм нахождения множителя позволяет более точно учитывать эти влияния и проводить более надежные и точные эксперименты.
Таким образом, алгоритм нахождения множителя для вычисления объема металла по способу Архимеда имеет широкое практическое применение и может быть полезен во многих отраслях, связанных с металлами и их обработкой.
Вопрос-ответ

Как работает алгоритм нахождения множителя для вычисления объема металла по способу Архимеда?
Алгоритм нахождения множителя для вычисления объема металла по способу Архимеда основан на измерении разности веса металлического изделия в воздухе и в специальной жидкости. Для этого сначала измеряется вес изделия в воздухе, затем вес изделия погруженного в жидкость. Разность этих весов и является множителем, который позволяет вычислить объем металла.
Какие данные нужно знать для применения алгоритма нахождения множителя для вычисления объема металла по способу Архимеда?
Для применения алгоритма необходимо знать вес металлического изделия в воздухе и вес изделия погруженного в специальную жидкость. Также важно знать плотность этой жидкости. Исходя из этих данных можно вычислить разность весов и определить объем металла.
Какие преимущества есть у метода Архимеда для измерения объема металла?
Метод Архимеда имеет несколько преимуществ. Во-первых, он является достаточно точным и позволяет определить объем металла с высокой точностью. Во-вторых, данный метод применим к различным металлическим изделиям, не зависимо от их формы и размеров. В-третьих, для проведения измерений по методу Архимеда не требуется сложное оборудование, что делает его более доступным и экономичным в использовании.
Можно ли применить метод Архимеда для измерения объема других материалов, кроме металла?
Метод Архимеда в первую очередь разработан для измерения объема металла, однако его принципы могут быть использованы и для измерения объема других материалов. В этом случае необходимо знать плотность исследуемого материала и правильно выбрать жидкость, в которую будет погружаться изделие. Таким образом, метод Архимеда может быть адаптирован для измерения объема различных материалов.
