Швеллер – это прокатный стальной профиль, который опирается на две продольные пластинки, соединенные с помощью хомута. Применение швеллера в строительстве имеет свои особенности, в частности, в сопроматных расчетах. В данной статье рассмотрим задачи с швеллером и способы их решения.
Одной из основных особенностей швеллера является его форма. Распределение напряжений по сечению профиля имеет неоднородный характер, что требует учета при проведении сопроматных расчетов. Это особенно важно при расчете прогиба, устойчивости и других параметров конструкции, где необходимо учесть не только силовые воздействия, но и форму и геометрические характеристики профиля.
Сопромат задачи с швеллером можно решить с использованием различных методов. Для начала необходимо определить характеристики швеллера, такие как момент инерции, площадь сечения, модуль упругости и другие. Затем проводится анализ силовых воздействий на конструкцию: распределение нагрузки, точечные и равномерные нагрузки, моменты и многие другие параметры. Наконец, основываясь на полученных данных, проводятся сопроматные расчеты, которые позволяют оценить прочность и устойчивость конструкции с швеллером.
Важно отметить, что сопроматные расчеты должны проводиться с учетом специфики применяемых материалов и методов соединения элементов конструкции. Также следует учитывать требования нормативных документов, которые регламентируют проектирование и строительство конструкций с применением швеллера. В случае сомнений и сложности в расчетах рекомендуется обращаться к специалистам.
Сопромат задачи: особенности и решения с швеллером
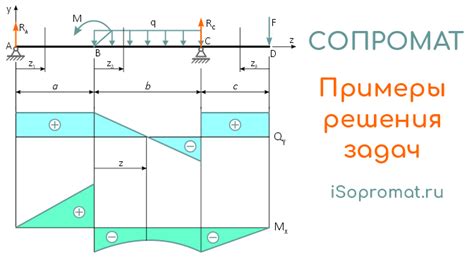
Швеллер - это вид стального профиля, широко используемого в строительстве и машиностроении. Он имеет форму буквы "С", что обеспечивает ему высокую прочность при небольшом весе. В задачах по сопромату швеллер также играет важную роль и требует особого внимания при решении.
Одной из особенностей задач с швеллером является необходимость учета его геометрических характеристик, таких как ширина полки, высота и толщина стенки. Эти параметры определяют его прочность и способность переносить нагрузку. Поэтому, при решении задач с швеллером, необходимо учитывать эти параметры и правильно применять формулы для расчета.
Для успешного решения задач с швеллером также важно учитывать место его применения и условия эксплуатации. Например, в случае строительства, швеллер может использоваться в качестве балки или столба. В зависимости от этого, применяются разные методы расчета и учитываются разные факторы, такие как длина балки, нагрузка на нее и ее удаление от оси швеллера.
Решение задач с швеллером также может включать проверку на устойчивость конструкции. Устойчивость означает, что швеллер способен сохранять свою форму и прочность при действии нагрузки. Для этого необходимо рассчитать его критическую силу, которая определяется формулами и зависит от геометрических характеристик швеллера и материала, из которого он изготовлен.
Таким образом, задачи с швеллером имеют свои особенности и требуют внимательного расчета и анализа. Важно учитывать геометрические характеристики швеллера, условия его применения и проверять устойчивость конструкции. Соблюдение этих условий позволит получить надежное и безопасное решение задачи с швеллером.
Особенности решения сопромат задач с применением швеллера

Швеллер - это конструкционный элемент изготовленный из стальных листов со скошенными краями. Он широко применяется в инженерных конструкциях, и решение сопромат задач с его использованием имеет свои особенности.
Первая особенность состоит в том, что при анализе швеллера необходимо учитывать не только его геометрические параметры, но и свойства материала, из которого он изготовлен. Например, швеллеры могут быть выполнены из различных видов стали, которые имеют разную прочность и упругость. В зависимости от выбранного материала, необходимо использовать соответствующие формулы и значения для расчета напряжений и деформаций.
Вторая особенность связана с учетом влияния различных нагрузок на швеллер. Швеллер может быть подвержен различным видам нагрузок, включая осевую нагрузку, изгибающий момент, срез и комбинированные нагрузки. Расчет сопротивления швеллера зависит от вида нагрузки и ее точного расположения на элементе. Кроме того, при анализе швеллера необходимо учитывать его длину и условия его закрепления.
Третья особенность состоит в том, что для анализа и расчета швеллера могут применяться различные методы, включая метод сечений, метод напряжений и метод деформаций. Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода зависит от конкретной задачи и ее условий.
Оптимальное решение сопромат задач с применением швеллера достигается путем правильного выбора материала и геометрии элемента, а также вычисления соответствующих напряжений и деформаций. Правильный расчет и анализ позволяют обеспечить надежность и безопасность конструкций, где используется швеллер.
Правильные подходы к решению задач с швеллером в сопромат
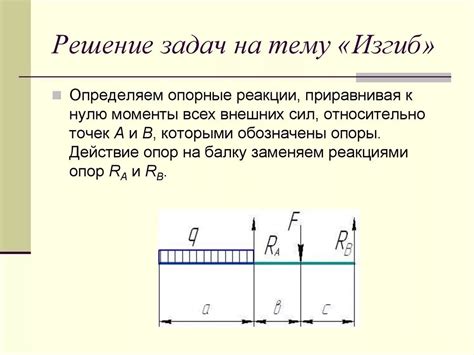
Решение задач с швеллером в сопромат требует правильного подхода и использования соответствующих методов анализа. Важно учитывать особенности геометрии и поведения швеллера, а также правильно определить условия нагрузки.
Вначале необходимо провести расчеты для определения внутренних усилий и напряжений в швеллере. Для этого применяются методы статического анализа, на основе которых можно определить действующие моменты, силы и перерезывающие силы.
Далее следует провести проверку прочности швеллера. Важно учесть материал и геометрию швеллера, а также применяемые допущения. Для этого можно использовать различные методы расчета прочности, такие как методы предельного состояния или методы работы предельного прогиба.
Особое внимание следует уделить устойчивости швеллера. Необходимо проверить его устойчивость относительно бокового смещения, изгиба и критической нагрузки. Для этого применяются различные методы анализа устойчивости, включая методы Эйлера и Колесова.
При решении задач с швеллером в сопромат необходимо учитывать все важные факторы, такие как геометрия, нагрузка, прочность и устойчивость. Для получения более точных результатов рекомендуется использовать программное обеспечение для расчета и анализа конструкций.
Примеры решения сопромат задач с применением швеллера и результаты

Пример 1:
Пусть задача заключается в определении максимальной нагрузки, которую может выдержать конструкция из швеллера. Для решения данной задачи необходимо провести расчеты на прочность и устойчивость швеллера.
Сначала определяется максимальный момент сил, действующий на швеллер. Затем рассчитывается несущая способность швеллера по формуле, учитывающей его геометрические параметры и свойства материала. В результате получается значение, которое является максимально допустимым моментом сил для данного швеллера.
Результат:
После проведения расчетов получается конкретное значение максимальной нагрузки, которую может выдержать швеллер. Это значение можно сравнить с требуемой нагрузкой и определить, соответствует ли конструкция из швеллера заданным параметрам.
Пример 2:
Рассмотрим задачу о распределении нагрузки на конструкцию из швеллера. Предположим, что на швеллер действуют различные силы и моменты, и требуется определить, как они распределены по сечению швеллера.
Для решения данной задачи необходимо провести расчеты на напряжение в различных точках сечения. В результате получается распределение напряжений, которое позволяет определить участки швеллера, наиболее нагруженные.
Результат:
После проведения расчетов получается распределение нагрузки по сечению швеллера. Это распределение можно сравнить с допустимыми значениями напряжений для данного материала и определить, находится ли швеллер в пределах допустимых значений.
Вопрос-ответ

Какие особенности имеют задачи с швеллером в сопромате?
Задачи с швеллером в сопромате имеют свои особенности. Одной из них является несимметричная форма сечения швеллера. Также, швеллер имеет две боковые плоскости, которые могут находиться в разных плоскостях. Кроме того, у швеллера могут быть отверстия для болтов и сварные швы. Все эти особенности необходимо учитывать при решении задач с швеллером в сопромате.
Какие методы решения задач с швеллером в сопромате можно использовать?
Для решения задач с швеллером в сопромате можно использовать различные методы. Одним из них является метод сечений, который заключается в разбиении конструкции на отдельные сечения и рассмотрении равновесия каждого сечения. Еще одним методом является метод шарнирных реакций, который основан на предположении, что сварные швы и болты находятся в состоянии шарнира и не передают моменты и силы. Также, для решения задач с швеллером можно использовать методы виртуальных перемещений, метод клеток и другие.
