Двутавровые швеллеры – это один из самых распространенных типов прокатного профиля, который широко используется в строительстве для сооружения различных конструкций. Это металлический профиль, имеющий форму буквы "I" с двумя горизонтальными полками и вертикальным стержнем между ними.
Преимуществами использования двутавровых швеллеров являются их высокая прочность и надежность. Благодаря своей конструкции они могут выдерживать значительные нагрузки, что делает их идеальным решением для строительства различных сооружений. Кроме того, двутавровые швеллеры легко могут быть соединены друг с другом, что позволяет создавать конструкции различной сложности.
В статье мы рассмотрим примеры использования двутавровых швеллеров для решения задач различной сложности. Мы покажем, как этот тип профиля может быть применен для создания каркасов зданий, мостов, металлических конструкций, а также для усиления и ремонта существующих сооружений. Будут рассмотрены различные методы соединения двутавровых швеллеров, а также особенности их укладки и монтажа.
Что такое двутавровые швеллеры

Двутавровые швеллеры представляют собой строительные элементы, широко применяемые в современном строительстве благодаря своим прочностным характеристикам и универсальности использования.
Они представляют собой металлические профили с двумя поперечными стенками и параллельными гранями, которые напоминают букву "Ш". За счет своей формы и структуры, двутавровые швеллеры обладают высокой несущей способностью и могут выдерживать значительные нагрузки, как в осевом, так и поперечном направлении.
Двутавровые швеллеры применяются в различных областях строительства и металлообработки, в том числе для изготовления металлических конструкций, каркасов зданий и сооружений, мостов, а также в производстве строительных металлоконструкций.
Изготавливают двутавровые швеллеры из стали методом горячей прокатки. Стандартизованы размеры и габариты швеллеров, что облегчает их применение в различных проектах и позволяет легко подобрать нужные элементы для конкретной цели. Диапазон размеров швеллеров позволяет выбрать оптимальное решение в зависимости от нагрузок и требований проекта.
Преимущества использования двутавровых швеллеров

1. Прочность и надежность. Двутавровый швеллер является одним из самых прочных элементов в конструкции. Он способен выдерживать высокие нагрузки и не деформироваться при эксплуатации. Благодаря своей конструкции, он обладает высокой устойчивостью к механическим воздействиям и стойкостью к коррозии.
2. Универсальность. Двутавровые швеллеры широко применяются в различных отраслях, включая строительство, машиностроение и мостостроение. Они могут использоваться в качестве основных структурных элементов, а также как поддерживающие элементы, для создания ферм, колонн, стропильных систем и других конструкций. Благодаря своей универсальности, двутавровые швеллеры позволяют создавать разнообразные конструкции с высокими требованиями к прочности и устойчивости.
3. Легкость монтажа. Использование двутавровых швеллеров упрощает процесс монтажа и сборки конструкции. Они имеют специальные отверстия для крепления к другим элементам конструкции, что облегчает и ускоряет процесс сборки. Кроме того, их легко обрабатывать и подгонять под нужную форму, что позволяет создавать индивидуальные и сложные конструкции.
4. Экономически эффективное решение. Использование двутавровых швеллеров позволяет сократить затраты на материалы и снизить время на монтаж. Благодаря своей высокой прочности и долговечности, они требуют минимального технического обслуживания и не нуждаются в замене на протяжении длительного времени. Это позволяет снизить эксплуатационные расходы и увеличить срок службы конструкции.
Итак, использование двутавровых швеллеров предоставляет ряд преимуществ, таких как прочность и надежность, универсальность, легкость монтажа и экономическая эффективность. Они являются незаменимыми элементами при строительстве и различных инженерных решениях, обеспечивая высокую прочность и устойчивость конструкции.
Определение категорий задач
Задачи, связанные с использованием двутавровых швеллеров, можно разделить на несколько категорий в зависимости от их характера и целей. Рассмотрим основные из них:
Проектирование конструкций с двутавровыми швеллерами. В данной категории задач требуется определить оптимальные параметры двутаврового швеллера, учитывая загрузки, условия эксплуатации и требования прочности. Инженерам необходимо провести расчеты на прочность и устойчивость конструкции, а также спроектировать систему креплений и соединений.
Использование двутавровых швеллеров в строительстве. В этой категории задач рассматривается применение двутавровых швеллеров при возведении зданий, сооружений и промышленных объектов. Инженеры должны определить необходимое количество и типы двутавровых швеллеров, разработать схему укладки и расположения элементов, а также обеспечить их надежное крепление.
Ремонт и усиление конструкций с использованием двутавровых швеллеров. В этой категории задач требуется провести оценку состояния существующих конструкций, определить необходимость ремонта или усиления. Инженеры должны выбрать оптимальные размеры и типы двутавровых швеллеров, разработать схему их установки, а также обеспечить правильное соединение с существующей конструкцией.
Эксплуатация и обслуживание двутавровых швеллеров. В данной категории задач требуется разработать планы по регулярному осмотру, обслуживанию и ремонту двутавровых швеллеров. Инженеры должны определить оптимальные сроки и методы проведения работ, а также обеспечить безопасность персонала в процессе эксплуатации конструкций.
Каждая из этих задач требует специальных знаний и навыков в области проектирования и конструирования с использованием двутавровых швеллеров. Решение этих задач позволяет обеспечить надежность, прочность и устойчивость конструкций, а также продлить их срок службы.
Статические задачи

Статические задачи в контексте решения задач с использованием двутавровых швеллеров связаны с определением оптимальных размеров и конструкции швеллера для обеспечения необходимой прочности и устойчивости конструкции.
При решении статических задач необходимо учитывать различные факторы, такие как нагрузка, прогибы, напряжения, устойчивость и деформации. При определении размеров швеллера необходимо рассчитать его сечение, учитывая данные о нагрузках и требуемых характеристиках прочности.
Одним из ключевых параметров, которые необходимо учитывать при решении статических задач, является момент инерции сечения швеллера. Он определяет его способность противостоять прогибам и деформациям под действием нагрузок. Чем больше момент инерции, тем более жесткая и устойчивая конструкция получится.
Другим важным параметром является площадь поперечного сечения швеллера. Она напрямую влияет на его прочность и способность принимать нагрузки. Площадь поперечного сечения должна быть достаточной для обеспечения безопасности конструкции и устойчивости ее работы.
Применение двутавровых швеллеров в решении статических задач позволяет создавать прочные и устойчивые конструкции, которые могут быть использованы в различных отраслях промышленности, строительстве и машиностроении. Правильный подбор размеров и конструкции швеллера позволяет создавать надежные и безопасные конструкции с минимальными затратами на материалы.
Динамические задачи
Динамические задачи являются распространенным видом задач, которые включают в себя движение или действие объектов. Они требуют решения с использованием двутавровых швеллеров, которые обладают высокой прочностью и устойчивостью.
Одна из распространенных динамических задач, в которых используются двутавровые швеллеры, - это задачи динамики механических систем. Например, для решения задачи о движении тела по наклонной плоскости с использованием двутаврового швеллера необходимо учесть силы трения и удерживающие силы, чтобы определить движение и скорость тела.
Другой тип динамической задачи, в которой используются двутавровые швеллеры, - это задачи о полете и падении объектов. Например, для решения задачи о падении тела с высоты с использованием двутаврового швеллера необходимо учесть гравитационную силу и силу сопротивления воздуха, чтобы определить время падения и скорость объекта при падении.
Еще одним примером динамической задачи является задача о равномерном движении объекта. Например, для решения задачи о движении автомобиля с использованием двутаврового швеллера необходимо учесть силу трения и силу сопротивления воздуха, чтобы определить скорость и время, необходимое автомобилю для преодоления определенного расстояния.
Все эти задачи требуют анализа сил и учета движения или изменений состояния объектов. Двутавровые швеллеры обладают достаточной прочностью и устойчивостью, чтобы решить эти задачи и обеспечить безопасность и надежность в конструкции. Поэтому использование двутавровых швеллеров является неотъемлемой частью решения динамических задач.
Примеры решения задач

Рассмотрим пример решения задачи на определение грузоподъемности двутаврового швеллера. Предположим, что у нас имеется двутавровый швеллер марки Б22, длина которого составляет 4 метра. Найдем максимально допустимую нагрузку, которую данный швеллер способен выдержать.
Исходя из технических характеристик швеллера марки Б22, знаем, что его вес составляет 22,3 кг/м. Следовательно, общая масса швеллера будет равна 22,3 кг/м * 4 м = 89.2 кг. Но для определения грузоподъемности необходимо учесть дополнительные факторы.
Для расчета грузоподъемности швеллера необходимо учесть влияние распределенной нагрузки, концентрированной нагрузки и изгибающего момента. В данном случае, учитывая длину швеллера и его особенности, рассчитываем грузоподъемность исходя из осевой нагрузки.
Для швеллеров марки Б22, предел прочности составляет 270 МПа. Посчитаем максимальный вес, который данный швеллер способен выдержать, используя формулу:
Грузоподъемность = (Предел прочности * Площадь поперечного сечения) / Запас прочности
Для швеллера марки Б22 площадь поперечного сечения составляет 4172 мм². Коэффициент запаса прочности выбирается в зависимости от условий эксплуатации и составляет 1,2. Подставляя значения в формулу, получаем:
Грузоподъемность = (270 МПа * 4172 мм²) / 1,2 = 926.5 кг
Таким образом, данное решение позволяет определить, что двутавровый швеллер марки Б22, длиной 4 метра, способен выдерживать максимально допустимую нагрузку весом 926.5 кг.
Расчет прогиба двутаврового швеллера
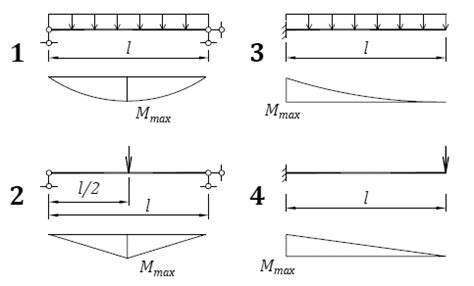
Расчет прогиба двутаврового швеллера является важной задачей в инженерном проектировании. Прогиб - это изгибная деформация, которая возникает под воздействием нагрузки на элемент конструкции. В случае двутаврового швеллера, прогиб может привести к его деформации или даже разрушению, поэтому расчет прогиба является необходимым этапом проектирования.
Для расчета прогиба двутаврового швеллера необходимо учитывать его геометрические параметры, материал изготовления и приложенную нагрузку. Основными параметрами для расчета прогиба являются длина швеллера, момент инерции поперечного сечения, модуль упругости материала и величина приложенной нагрузки.
Расчет прогиба можно выполнить с использованием различных методов. Один из способов - это использование теории балки, которая позволяет определить максимальный прогиб швеллера под приложенной нагрузкой. Для этого необходимо знать значения всех параметров и воспользоваться уравнением, которое связывает прогиб, приложенную нагрузку и другие характеристики швеллера.
После расчета прогиба двутаврового швеллера можно провести его сравнение с допустимыми значениями. Допустимый прогиб определяется на основе требований нормативно-технической документации и безопасности конструкции. Если результат расчета превышает допустимое значение, необходимо произвести коррекцию параметров или выбрать швеллер с большей жесткостью.
Расчет прочности двутаврового швеллера

Двутавровый швеллер - это прокатный профиль, который широко применяется в строительстве и машиностроении. Когда проект предусматривает использование двутавровых швеллеров, очень важно выполнить расчет прочности данного элемента конструкции. Расчет прочности двутаврового швеллера позволяет убедиться в его способности выдерживать механические нагрузки при эксплуатации.
В расчете прочности двутаврового швеллера учитывается несколько факторов. Важными параметрами являются геометрические размеры профиля, материал изготовления и характеристики механических свойств материала. В зависимости от конкретной задачи, расчет прочности может проводиться в различных направлениях, таких как продольное или поперечное направление.
Для проведения расчета прочности двутаврового швеллера используются различные методы. Одним из основных методов является метод конечных элементов, который позволяет учесть сложные геометрические параметры и различные вариации нагрузок. Также в расчете прочности можно использовать методы аналитической механики и сопоставление полученных результатов с нормативными значениями из соответствующих стандартов.
Проведение расчета прочности двутаврового швеллера позволяет определить, является ли данный элемент конструкции достаточно прочным для выполнения заданных функций. Результаты расчета позволяют принять решение о выборе оптимального варианта применения двутаврового швеллера в проекте, а также проверить его безопасность при различных условиях эксплуатации.
Вопрос-ответ

Какие материалы можно использовать для решения задач с использованием двутавровых швеллеров?
Для решения задач с использованием двутавровых швеллеров можно использовать различные материалы, включая сталь, алюминий и другие сплавы.
Какой тип задач можно решить с использованием двутавровых швеллеров?
Двутавровые швеллеры могут быть использованы для решения различных задач, таких как строительство зданий, мостов и других инженерных сооружений.
Какие преимущества имеют двутавровые швеллеры по сравнению с другими конструкциями?
Двутавровые швеллеры обладают рядом преимуществ, включая высокую прочность, устойчивость к деформации, возможность поддерживать большой вес и легкость монтажа.
Как выбрать правильный размер двутаврового швеллера для задачи?
Выбор правильного размера двутаврового швеллера зависит от нескольких факторов, включая ожидаемую нагрузку, длину пролета и другие технические требования. Рекомендуется проконсультироваться с инженером или специалистом в этой области, чтобы подобрать оптимальный размер.
