Гибка металла является важным процессом в производстве, который позволяет превратить плоские листы металла в изделия с заданной формой и размерами. Один из ключевых факторов, определяющих качество гибки и конечный результат, - это матрица. Матрица - это специально изготовленные формы, которые придают металлическому листу нужную форму и угол гиба.
Основной принцип работы матрицы для гибки металла состоит в том, что приложенная к металлическому листу сила и ее направление определяют форму и угол гиба. Матрица, в свою очередь, обеспечивает поддержку и контроль процесса гибки, предотвращая деформации и повреждения металла. Она должна быть достаточно прочной и жесткой, чтобы выдерживать приложенную силу и не деформироваться.
Для расчета матрицы для гибки металла применяются различные методы и алгоритмы. Один из них - метод конечных элементов, который основывается на разбиении самой матрицы и гибкого листа на конечные элементы и последующем анализе напряжений, деформаций и других параметров в каждом элементе. Такой подход позволяет более точно предсказать поведение материала в процессе гибки и улучшить конструкцию и форму матрицы.
Инженеры и проектировщики, занимающиеся гибкой металла, должны учесть множество факторов при расчете матрицы. Это и физические свойства металла, и геометрические характеристики, и требования к конечному изделию. Задача состоит в том, чтобы найти оптимальную форму и размеры матрицы, которая обеспечат качественную гибку без деформаций и повреждений металла.
В итоге, правильно разработанная и рассчитанная матрица для гибки металла играет важную роль в процессе производства, гарантируя высокое качество и точность готовых изделий. Освоение принципов и методов расчета матрицы для гибки металла требует определенных знаний и навыков, но оправдывает себя в виде повышенной производительности, снижении затрат и улучшении качества продукции.
Основные принципы расчета матрицы для гибкого металла
Расчет матрицы для гибкого металла является важным этапом в процессе изготовления изделий из металла методом гибки. Основные принципы этого расчета включают учет механических свойств материала, определение необходимой гибкости и удержания формы изделия, а также оценку деформаций и напряжений, возникающих в процессе гибки.
Первым шагом в расчете матрицы является анализ свойств гибкого металла, таких как его твердость, пластичность и упругость. Это позволяет определить оптимальные параметры матрицы, такие как материал и толщина, чтобы обеспечить правильную гибкость и удержание формы изделия.
Вторым шагом является определение требуемой гибкости матрицы. Она должна быть достаточной для формирования нужной геометрии изделия, но при этом не должна быть такой высокой, чтобы вызвать разрушение материала или появление нежелательных деформаций. Это требует тщательного анализа геометрии изделия, его размеров и особенностей конструкции.
Третьим шагом является оценка деформаций и напряжений, возникающих в материале в процессе гибки. Для этого применяются различные методы анализа, такие как численное моделирование, экспериментальные испытания и расчеты с использованием теоретических моделей. Основной целью является определение оптимальной формы и размеров матрицы, чтобы минимизировать деформации и напряжения в изделии.
В заключение, расчет матрицы для гибкого металла требует комплексного подхода, учета механических свойств материала, определения требуемой гибкости и оценки деформаций и напряжений. Только таким образом можно обеспечить высокое качество изделий и улучшить процесс изготовления металлических конструкций методом гибки.
Технология гибки металла

Технология гибки металла является важным процессом в производстве различных изделий из металла. В основе этой технологии лежит использование специального оборудования, которое способно придавать металлическим листам нужную форму и изгиб.
Одним из основных методов гибки металла является применение гибочного пресса. Это специальное оборудование позволяет приложить значительную силу к листу металла, давая возможность ему изменять свою форму. Чтобы достичь желаемой формы, при гибке металла используются различные инструменты, такие как матрицы и фланцы.
Важной частью технологии гибки металла является процесс выбора правильного материала. Материал должен быть достаточно прочным, чтобы выдерживать давление и изгибы, но при этом должен быть достаточно гибким, чтобы получить нужную форму. Поэтому производители металлических изделий тщательно выбирают материалы, чтобы обеспечить оптимальные результаты.
Технология гибки металла нашла применение в различных отраслях, включая автомобильную промышленность, машиностроение, электронику и даже строительство. Она позволяет создавать изделия с различными формами и размерами, а также обеспечивает высокую точность и качество готовых изделий.
В целом, технология гибки металла является важным процессом, который играет ключевую роль в производстве металлических изделий. Она позволяет обеспечить нужную форму и изгибы листам металла, что открывает широкие возможности для создания различных изделий, полезных во многих отраслях промышленности.
Значение матрицы в процессе гибки

Матрица является одной из ключевых составляющих в процессе гибки металла. Она представляет собой инструмент, с помощью которого создается желаемая форма заготовки.
Основное значение матрицы заключается в том, что она определяет конечную форму изделия. Матрица создает точки опоры и задает направление, в котором будет совершаться гибка. Она позволяет закрепить заготовку и удерживать ее на месте во время деформации.
Для получения желаемой формы заготовки необходимо выбрать правильную матрицу, учитывая такие параметры, как толщина и тип материала. Корректно подобранная матрица позволяет достичь высокой точности гибки и избежать возможных дефектов и искажений в изделии.
В процессе работы матрица подвергается значительным нагрузкам и износу. Поэтому важно регулярно проверять состояние матрицы и выполнять ее техническое обслуживание. Неправильное использование или изношенность матрицы может привести к неправильной гибке заготовки, повреждению материала или поломке оборудования.
В целом, матрица играет ключевую роль в процессе гибки металла, обеспечивая точность и качество изделия. Правильный выбор, использование и обслуживание матрицы являются важными факторами для успешной реализации задач по гибке металла.
Основные методы расчета матрицы

1. Эмпирический метод. Данный метод основан на опыте и наблюдениях предшествующих исследований. В ходе этого метода используются статистические данные и прецеденты для расчета параметров матрицы гибки металла. Однако эмпирический метод имеет недостаток в том, что он не всегда может учесть все возможные варианты и особенности материала.
2. Аналитический метод. Данный метод основан на математических моделях и уравнениях, которые позволяют определить структуру и свойства матрицы. Аналитический метод позволяет получить точные результаты, но при этом требует высокой квалификации и опыта у исследователя.
3. Численный метод. Данный метод использует численные алгоритмы и симуляции для расчета матрицы. С помощью компьютерного моделирования можно учесть множество факторов, таких как напряжение, деформации и температура, что делает численный метод очень точным и эффективным.
4. Статистический метод. Данный метод основан на анализе статистических данных и вероятностных моделей. С его помощью можно оценить риски и вероятность возникновения различных факторов, таких как повреждения и износ матрицы.
5. Экспертный метод. Данный метод основан на мнении и опыте экспертов в области гибки металла. Эксперты могут предоставить ценную информацию и советы при выборе и настройке матрицы.
6. Комбинированный метод. Данный метод основан на сочетании различных методов расчета матрицы. Это позволяет получить наиболее точные и надежные результаты и учесть различные аспекты структуры и свойств матрицы гибки металла.
Математические модели для расчета матрицы

Для расчета матрицы в процессе гибки металла используются различные математические модели, которые позволяют определить напряжения и деформации в материале. Одной из основных моделей является модель теории пластичности. Она основана на предположении о том, что деформации металла происходят при постоянных напряжениях, а после устранения нагрузки материал остается пластически деформированным.
Еще одной распространенной моделью является модель конечных элементов. Она основана на разбиении исследуемого объекта на множество маленьких элементов, каждый из которых описывается своими характеристиками напряжений и деформаций. Затем происходит численное решение уравнений, описывающих поведение каждого элемента, и получение итогового распределения напряжений и деформаций в материале.
Также применяются методы аналитической механики для расчета матрицы. Они основаны на использовании уравнений равновесия, законов сохранения массы и импульса, а также аналитических выражений для описания поведения материала в процессе гибки. Однако эти методы используются в основном для расчета простых геометрических форм, так как они требуют аналитических решений и не всегда применимы для сложных объектов.
В целом, выбор математической модели для расчета матрицы зависит от сложности объекта и требуемой точности результата. Каждая модель имеет свои преимущества и недостатки, и ее выбор определяется индивидуально для каждой конкретной задачи.
Использование компьютерных программ для расчета матрицы

Расчет матрицы для гибки металла является сложным процессом, требующим высокой точности и большого объема вычислений. В настоящее время большинство специалистов применяют компьютерные программы для выполнения таких расчетов.
Специальные программы для расчета матрицы позволяют проводить анализ и моделирование процесса гибки металла с использованием различных параметров. Они учитывают такие факторы, как материал металла, его толщина, радиус гибки, угол гибки и другие параметры.
Компьютерные программы позволяют специалистам проводить расчеты с высокой степенью точности, учитывая все физические свойства материала и условия процесса гибки. Они позволяют определить оптимальные параметры для достижения требуемого результата и предсказать поведение материала в процессе гибки.
Кроме того, компьютерные программы облегчают процесс проектирования и моделирования матрицы для гибки металла. Они позволяют создавать 3D-модели матрицы, проводить виртуальное тестирование и оптимизировать ее дизайн. Такой подход позволяет сократить время и затраты на создание и испытания физического прототипа матрицы.
Использование компьютерных программ для расчета матрицы увеличивает эффективность и точность процесса гибки металла. Он позволяет специалистам быстро и точно определить параметры матрицы и прогнозировать ее поведение, что способствует повышению качества и надежности гибки металла.
Критерии оценки качества матрицы
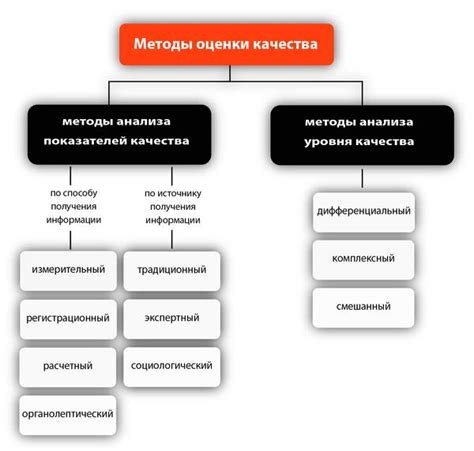
Оценка качества матрицы для гибки металла является важным шагом в процессе ее разработки и производства. Эффективность и долговечность матрицы напрямую влияют на качество конечного продукта и производительность процесса гибки. Для определения качества матрицы используются различные критерии, учитывающие не только ее прочность, но и другие важные параметры.
Один из основных критериев оценки качества матрицы - это ее точность. Точность определяется способностью матрицы сохранять геометрические размеры и форму продукта в процессе гибки. Чем более точна матрица, тем меньше будет искажение формы и размеров конечного изделия. Это особенно важно при производстве сложных и точных деталей.
Еще одним важным критерием является износостойкость матрицы. В процессе гибки металла матрица подвергается значительным механическим нагрузкам, что может приводить к ее износу. Износостойкость определяется материалом, из которого изготовлена матрица, а также ее конструкцией и обработкой. Матрица должна быть способна выдержать большое количество циклов гибки без потери своих характеристик.
Другим важным критерием является стабильность матрицы. Стабильность определяется ее способностью сохранять свои характеристики и геометрическую форму при различных условиях эксплуатации. Матрица должна быть устойчива к изменениям температуры, силам и вибрациям, чтобы обеспечивать стабильность процесса гибки и качество конечного изделия.
Наконец, одним из важных критериев является стоимость матрицы. При разработке и производстве матрицы учитываются затраты на материалы, оборудование, технологические процессы и трудозатраты. Рациональное соотношение между качеством и стоимостью позволяет достичь наилучшего результата при разработке и производстве матрицы для гибки металла.
Вопрос-ответ

Какие основные принципы использования матрицы для гибки металла?
Основными принципами использования матрицы для гибки металла являются правильный выбор материала матрицы, определение оптимальной формы и размеров, учет технологических характеристик материала, правильная установка и закрепление матрицы, а также соблюдение тщательных методов обработки.
Какие методы расчета матрицы используются для гибки металла?
Для расчета матрицы при гибке металла применяются различные методы, включая аналитические и численные. Аналитические методы основаны на использовании теоретических моделей и уравнений, которые позволяют предсказать поведение материала при гибке. Численные методы, такие как метод конечных элементов, позволяют проводить более точные и комплексные расчеты, учитывая нелинейные свойства материала и сложную геометрию детали.
Какую роль играет матрица при гибке металла?
Матрица играет ключевую роль при гибке металла, так как она обеспечивает нужную форму и размеры детали. Она служит опорой для металла и контролирует его деформацию, предотвращает образование трещин и дефектов. Матрица должна обладать достаточной прочностью и жесткостью, чтобы выдерживать нагрузки, возникающие при гибке, а также гладкой поверхностью, чтобы избежать повреждения детали.
