Классическая электронная теория проводимости металлов является одной из основных теорий, которая пытается объяснить, как электрический ток передвигается в металлах. Она основана на представлении о свободных электронах в металле, которые передвигаются в электрическом поле. Однако, несмотря на свою успешность в объяснении многих явлений, классическая электронная теория имеет свои недостатки, которые требуют более глубокого исследования.
Один из основных недостатков классической электронной теории проводимости металлов заключается в том, что она не учитывает квантовые эффекты и корпускулярно-волновую природу электронов. В классической электронной теории электроны рассматриваются как классические частицы, которые могут свободно перемещаться в металле. Однако в квантовой механике электроны описываются волновыми функциями, которые определяют вероятность нахождения электрона в определенном состоянии.
Кроме того, классическая электронная теория не учитывает взаимодействие электронов между собой и с решеткой металла. В классической теории электроны рассматриваются независимо друг от друга и не взаимодействуют друг с другом. Однако в реальности электроны в металле взаимодействуют друг с другом через электромагнитные силы и также взаимодействуют с атомами решетки.
В итоге, недостаточность классической электронной теории проводимости металлов требует разработки и использования более сложных моделей, которые учитывают квантовые эффекты и взаимодействие электронов. Такие модели могут помочь более точно описать проводимость металлов и объяснить многие наблюдаемые явления в электрических свойствах металлов.
Классическая электронная теория

Классическая электронная теория проводимости металлов является одной из основных моделей, используемых для объяснения электропроводности в металлах.
Согласно этой теории, проводимость металлов объясняется движением свободных электронов, которые приложением электрического поля начинают двигаться в направлении противоположном полю. Этот эффект называется дрейфом электронов. Свободные электроны в металлах характеризуются своей подвижностью, которая определяется столкновениями электронов с зарядами и средой.
Классическая электронная теория также объясняет эффект сопротивления металлов, которое возникает из-за столкновений электронов с ионами металлической решетки. Чем больше столкновений, тем больше сопротивление металла. Таким образом, классическая электронная теория позволяет качественно описывать явления электропроводности в металлах.
Однако, классическая электронная теория имеет свои недостатки. В частности, она не может объяснить некоторые особенности поведения электронов в металлах, такие как явление сверхпроводимости и эффекты, связанные с квантовыми свойствами электронов. В связи с этим, для более полного описания поведения электронов в металлах были разработаны квантовомеханические модели, которые учитывают эффекты квантовой статистики и волнового характера электронов.
Ограничения классической электронной теории проводимости металлов
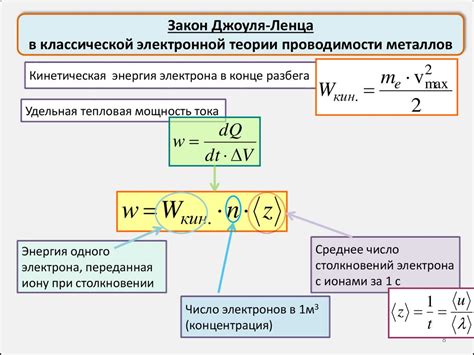
Классическая электронная теория проводимости металлов успешно объясняет множество явлений в металлических материалах, однако она имеет свои ограничения и не может полностью описать некоторые важные аспекты проводимости.
Одним из основных ограничений классической электронной теории является игнорирование ядерных эффектов. В этой теории предполагается, что электроны свободно двигаются в фоне положительно заряженного ионного решетки без взаимодействия с ядрами. Однако в реальности существуют сильные ядерные эффекты, такие как рассеяние электронов на ядрах, влияющие на проводимость.
Еще одним ограничением классической электронной теории является неучет квантовых эффектов. В классической теории электронное состояние описывается непрерывным спектром энергии, однако на микроскопическом уровне электроны обладают корпускулярно-волновыми свойствами и их энергия квантуется. Это означает, что в определенных условиях электроны могут проявлять волновую природу, что влияет на транспортные свойства и проводимость металлов.
Также классическая электронная теория не учитывает эффекты сверхпроводимости и металлического сопротивления. В сверхпроводниках электрический ток может протекать без потерь энергии, а в металлах сопротивление может возникать из-за рассеяния электронов на дефектах и примесях. Эти явления остаются за рамками классической электронной теории и требуют использования квантовомеханических подходов для их объяснения.
Квантовая механика и ее влияние на теорию проводимости

Квантовая механика является основным фундаментом современной физики и оказывает значительное влияние на теорию проводимости металлов. В отличие от классической электронной теории, которая основывается на предположении о непрерывности электронных состояний и их свободном движении, квантовая механика учитывает волновую природу электронов и их дискретные энергетические уровни.
Согласно квантовой механике, электроны в металле могут существовать только на определенных энергетических уровнях, называемых квантовыми состояниями. Каждое квантовое состояние характеризуется определенными значениями энергии, импульса и магнитного момента. Кроме того, электроны подчиняются принципу запрета Паули, согласно которому в одном квантовом состоянии могут находиться не более одного электрона.
Квантовая механика вносит существенные изменения в понимание явления проводимости металлов. Она позволяет более точно описывать поведение электронов в проводниках и объяснять такие явления, как электрическое сопротивление, термоэлектрические свойства и магнетооптические эффекты. Кроме того, квантовая механика позволяет учесть квантовые эффекты, такие как квантовая интерференция или туннелирование, которые играют важную роль в наноэлектронике и квантовых приборах.
Таким образом, квантовая механика является неотъемлемой частью современной теории проводимости металлов и позволяет более глубоко понять и объяснить множество физических явлений, связанных с проводимостью электричества в металлах.
Квантовые эффекты в металлах и их последствия

Классическая электронная теория проводимости металлов не учитывает квантовые эффекты, которые могут иметь значительное влияние на поведение электронов в металлах. Одним из таких эффектов является квантовая туннелирование, когда электроны могут переходить через потенциальные барьеры, которые они классически не могли бы пройти. Это может приводить к феномену, известному как туннельная проводимость.
Другим квантовым эффектом является квантовая интерференция, когда электроны могут проявлять волновые свойства и взаимодействовать друг с другом, образуя интерференционные максимумы и минимумы. Это может приводить к изменению проводимости материала и возникновению новых эффектов.
Квантовые эффекты также могут приводить к изменению электрической и тепловой проводимости металлов. Например, электроны могут испытывать рассеяние на квантовых дефектах, таких как дефекты кристаллической решетки или примеси. Это может привести к увеличению сопротивления материала и ухудшению его проводимости.
Квантовые эффекты играют важную роль в наноструктурах и низкоразмерных системах, где размеры объектов становятся сравнимыми с длиной волны электронов. В таких системах квантовые эффекты могут приводить к появлению квантовых точек, проводимости по краям и другим интересным эффектам.
Изучение и понимание квантовых эффектов в металлах и их последствий является важной задачей современной физики и материаловедения. Это позволяет не только лучше понять поведение электронов в металлах, но и использовать квантовые эффекты для создания новых материалов и устройств с улучшенными свойствами проводимости.
Применение квантовой теории в современных исследованиях
Квантовая теория играет важную роль в современных исследованиях в области физики и материаловедения. Благодаря своим уникальным принципам, она позволяет изучать микро- и наноструктуры материалов, а также объяснять различные явления, которые не могут быть полностью и точно описаны классической физикой.
Одной из областей, в которой квантовая теория находит широкое применение, является исследование проводимости металлов. Классическая электронная теория не может объяснить некоторые наблюдаемые явления, такие как низкотемпературная проводимость и квантовые эффекты в наноразмерных структурах.
Квантовая теория проводимости позволяет рассматривать электроны в металлах как квантовые объекты, объяснять наличие энергетических уровней и эффект туннелирования. Она также позволяет учитывать взаимодействие электронов с кристаллической решеткой и другие факторы, которые влияют на электрическую проводимость металлов.
С помощью квантовой теории проводимости исследователи проводят эксперименты и моделируют различные сценарии проводимости. Например, они исследуют влияние наноструктур на электрическую проводимость и разрабатывают новые материалы с уникальными свойствами. Также квантовая теория помогает объяснить низкотемпературное поведение металлов, такое как сверхпроводимость.
В целом, применение квантовой теории в современных исследованиях позволяет более точно и полно понимать явления и свойства материалов, что открывает новые возможности для разработки новых технологий и материалов с улучшенными характеристиками.
Вопрос-ответ

Что такое классическая электронная теория проводимости металлов?
Классическая электронная теория проводимости металлов - это основная теоретическая модель, которая описывает, как свободные электроны движутся в металле под влиянием электрического поля.
В чем состоит недостаточность классической электронной теории проводимости металлов?
Недостаточность классической электронной теории проводимости металлов заключается в том, что она не может объяснить некоторые наблюдаемые явления в проводниках, такие как сопротивление и эффект Холла.
Какие явления не могут объясниться классической электронной теорией проводимости металлов?
К классической электронной теории проводимости металлов не могут быть применены понятия, объясняющие сопротивление, температурную зависимость проводимости и эффект Холла.
Что является основными положениями недостаточности классической электронной теории?
Основными положениями недостаточности классической электронной теории проводимости металлов являются необходимость учета взаимодействия электронов с кристаллической решеткой и квантовых эффектов при низких температурах.
