Металлы – это класс веществ, который имеет особые свойства, делающие их важными объектами изучения в физике. Одним из ключевых аспектов изучения металлов является разработка и использование формул, которые позволяют описать их физические и химические свойства.
Основные формулы металлов в физике включают законы, описывающие их проводимость, теплопроводность, магнитные свойства и другие важные характеристики. Например, формула Ома используется для расчета электрического сопротивления металлических проводников, а формула Фурье позволяет определить теплопроводность металлов.
Еще одной важной формулой металлов в физике является закон Кюри-Вейсса, который связывает магнитные свойства металлов со значением их температуры. Эта формула позволяет предсказать поведение магнитных материалов в зависимости от температуры и определить их критические точки.
Великой наукой является изучение металлов. Основные формулы позволяют полноценно описывать и предсказывать их свойства.
Независимо от области применения металлов, знание и использование основных формул в физике позволяет ученым и инженерам разрабатывать новые материалы, улучшать существующие и создавать инновационные технологии. С помощью этих формул можно оценить эффективность использования металлов в различных сферах, таких как энергетика, транспорт, медицина и многое другое.
Изучение основных формул металлов в физике является неотъемлемой частью образования в этой области и открывает безграничные возможности для исследования и применения металлов в нашей повседневной жизни.
Металлы в физике: основные формулы
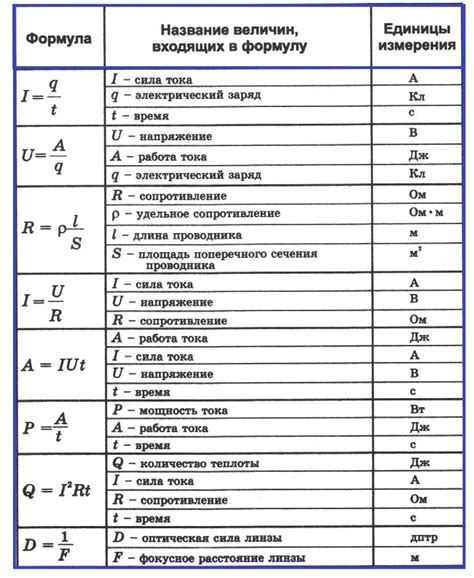
Металлы играют важную роль в физике и имеют множество основных формул, которые широко используются в этой науке.
- Плотность: Для металлов можно использовать формулу для расчета их плотности. Данная формула связывает массу и объем металла. Плотность металла рассчитывается как отношение массы к объему.
- Удельная теплоемкость: Эта формула связывает изменение теплоты вещества с его изменением температуры. Удельная теплоемкость металла определяется как отношение изменения теплоты к изменению температуры для заданной массы металла.
- Удельное сопротивление: Для металлов можно использовать формулу для расчета их удельного сопротивления. Удельное сопротивление металла рассчитывается как отношение его сопротивления к его сечению.
- Электромагнитная индукция: Металлы также обладают способностью создавать магнитное поле, и для расчета его индукции используется формула, которая связывает индукцию с силой и площадью проводника.
Эти формулы помогают ученым и обычным людям понять и применить свойства и законы, характеризующие металлы в физике. Они дают возможность рассчитывать и предсказывать различные параметры и свойства металлических материалов, что имеет большое практическое значение в настоящем и будущем.
Масса и объем металла
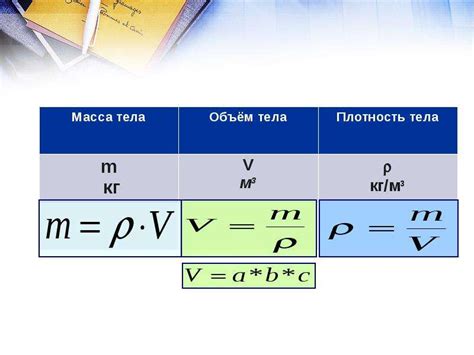
Масса металла является одной из основных характеристик, которая определяет его физические свойства. Масса металла измеряется в граммах или килограммах. Она обычно указывается в химических таблицах, а также может быть рассчитана с помощью специальных формул.
Объем металла также является важной характеристикой. Объем показывает, какое пространство металл занимает. Объем металла измеряется в кубических сантиметрах или кубических метрах. Его можно рассчитать по формуле, зная массу и плотность металла.
Масса и объем металла имеют важное значение при решении различных физических задач. Например, с помощью этих данных можно рассчитать плотность металла, которая показывает, насколько он плотный или легкий. Плотность металла рассчитывается делением его массы на объем.
Также масса и объем металла позволяют определить его плотность и применить это знание в решении различных инженерных задач. Например, зная плотность металла, можно рассчитать его массу, если известен его объем.
Плотность и средняя плотность металла

Плотность металла - это величина, определяющая массу единицы объема данного вещества. Она выражается в г/см³ или кг/м³. Плотность металла зависит от его атомной массы и структуры кристаллической решетки.
Для каждого металла плотность может быть различной. Например, плотность железа составляет около 7,86 г/см³, а плотность алюминия - около 2,7 г/см³. Эти значения могут быть полезны для расчетов при проектировании и изготовлении различных конструкций.
Однако плотность металла не является постоянной величиной и может изменяться в зависимости от условий. Например, при повышении температуры плотность металла обычно уменьшается. Это связано с увеличением расстояния между атомами при нагреве, что приводит к увеличению среднего объема занимаемого металлом.
Понятие средней плотности металла используется при изготовлении сплавов. Средняя плотность сплава вычисляется путем взвешивания нескольких его компонентов и вычисления соответствующей смешанной плотности. Такой подход применяется для определения плотности сплавов, состоящих из разных металлов или добавок.
Для удобства можно использовать таблицы, в которых указываются значения плотности различных металлов. Например, таблица плотности металлов содержит информацию о плотности алюминия, железа, меди, свинца и других распространенных металлов.
Удельная теплоемкость металла

Удельная теплоемкость — это физическая величина, которая определяет количество тепла, необходимого для нагрева единицы массы вещества на один градус Цельсия. Для металлов удельная теплоемкость является важным параметром, поскольку она позволяет определить, насколько быстро металл может нагреться или остыть.
Удельная теплоемкость металла зависит от таких факторов, как его химический состав, кристаллическая структура и температура. Некоторые металлы, такие как алюминий и медь, обладают высокой удельной теплоемкостью, что делает их хорошими теплоносителями. Другие металлы, например, железо и никель, имеют более низкую удельную теплоемкость, что означает, что они нагреваются и остывают быстрее.
Удельная теплоемкость металла может быть определена экспериментально или вычислена с помощью специальных формул. Для этого необходимо знать массу металла, его удельную теплоемкость и изменение температуры. Формула для расчета количества тепла, переданного металлу, выглядит следующим образом: Q = m * c * ΔT, где Q — количество тепла, m — масса металла, c — удельная теплоемкость металла и ΔТ — изменение температуры.
Знание удельной теплоемкости металла позволяет ученым и инженерам рассчитывать тепловые процессы при обработке и использовании металлов. Оно также имеет практическое значение при проектировании систем отопления, охлаждения и кондиционирования воздуха, где металлы часто используются в качестве материалов.
Удельная электропроводность металла
Удельная электропроводность металла – это физическая величина, которая характеризует способность материала проводить электрический ток. Она измеряется в ом*метр/метр (Ом·м/м) и обозначается символом σ.
Удельная электропроводность зависит от различных факторов, включая концентрацию свободных электронов и мобильность электронов внутри металлической решетки. Большая концентрация свободных электронов и высокая их мобильность способствуют высокой электропроводности металла.
Для большинства металлов удельная электропроводность является очень высокой, что делает их отличными проводниками электричества. Некоторые металлы, такие как медь и алюминий, имеют особенно высокую удельную электропроводность и широко используются в электротехнике и электронике.
Удельная электропроводность металлов может быть измерена с помощью специальных приборов, таких как удельной проводимости мост, который позволяет определить эту величину с высокой точностью. Знание удельной электропроводности металла является важным для проектирования и расчета электрических цепей и электронных устройств.
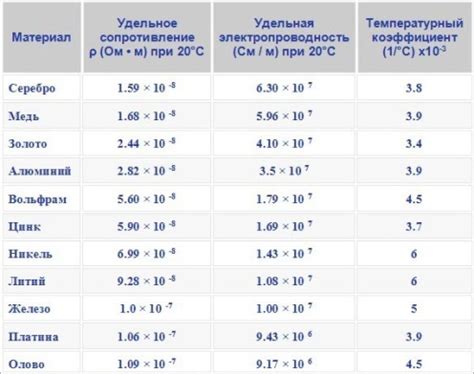
В таблице ниже приведены значения удельной электропроводности для некоторых распространенных металлов:
| Металл | Удельная электропроводность (Ом·м/м) |
|---|---|
| Медь | 5.96 × 10^7 |
| Алюминий | 3.77 × 10^7 |
| Железо | 1.0 × 10^7 |
| Серебро | 6.30 × 10^7 |
Из таблицы видно, что медь и серебро имеют самую высокую удельную электропроводность среди рассмотренных металлов.
Коэффициент линейного теплового расширения металла
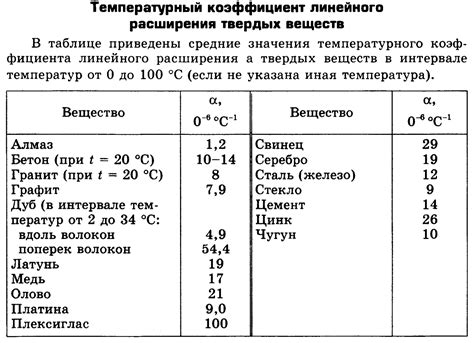
Коэффициент линейного теплового расширения металла – это физическая величина, которая характеризует изменение длины металла при изменении его температуры.
Коэффициент линейного теплового расширения обозначается символом α и измеряется в 1/°C или 1/K. Он определяется как относительное изменение длины материала на единицу длины при изменении его температуры на один градус.
Для различных металлов коэффициент линейного теплового расширения может быть разным. Например, у железа он составляет около 12×10^(-6) 1/°C, у алюминия – около 23×10^(-6) 1/°C, а у меди – около 17×10^(-6) 1/°C.
Коэффициент линейного теплового расширения является важным параметром при проектировании и изготовлении различных металлических конструкций, так как при изменении температуры они могут расширяться или сжиматься. Знание коэффициента линейного теплового расширения позволяет учитывать этот эффект и предотвращать деформации или разрушения конструкций.
Скорость звука в металле
Скорость звука в металле зависит от его физических свойств и состава. В общем случае, скорость звука в металлах выше, чем в воздухе, и может достигать нескольких километров в секунду.
Скорость звука в металле определяется его плотностью и модулями упругости. Плотность металла влияет на возможность передачи звуковых волн в нем: чем выше плотность, тем быстрее звук распространяется. Модули упругости металла связаны с его жесткостью и упругостью, и чем выше значения модулей упругости, тем выше скорость звука.
Скорость звука в металле может различаться в зависимости от его типа и структуры. Например, для металлов с простой кубической решеткой скорость звука может быть выше, чем для металлов с кольцевой или гексагональной решеткой.
Изучение скорости звука в металлах имеет практическое значение. Например, знание скорости звука позволяет определить состав и структуру материалов, а также применять металлы в различных областях, таких как строительство, авиация, машиностроение и другие промышленные отрасли.
Вопрос-ответ

Какие основные формулы металлов используются в физике?
В физике металлов используются различные формулы, включающие законы электромагнетизма, кристаллическую структуру, термодинамику и другие. Например, одной из основных формул является уравнение Эйнштейна, которое описывает зависимость между энергией, массой и скоростью света. Еще одной важной формулой является закон Ома, который описывает связь между напряжением, силой тока и сопротивлением в металле.
Какие законы электромагнетизма применяются в физике металлов?
В физике металлов применяются такие законы электромагнетизма, как закон Кулона, закон Гаусса, закон Ампера и закон Фарадея. Закон Кулона описывает взаимодействие зарядов и определяет силу электростатического взаимодействия между ними. Закон Гаусса позволяет рассчитать электрическое поле, создаваемое зарядами внутри замкнутой поверхности. Закон Ампера связывает магнитное поле с электрическим током, а закон Фарадея описывает явление электромагнитной индукции.
Какая формула описывает кристаллическую структуру металлов?
Одной из формул, описывающих кристаллическую структуру металлов, является формула Брэгга. Согласно этой формуле, для дифракции рентгеновских лучей на кристаллах выполняется условие максимального конструктивного вмешательства при определенных значениях углов падения и отражения. Формула Брэгга позволяет определить параметры кристаллической решетки металлов, такие как расстояние между плоскостями решетки и углы дифракции.
