Учебная программа по математике в 11 классе включает в себя разнообразные разделы, в том числе и изучение металлов. Математические модели и методы являются незаменимым инструментом для анализа и предсказания свойств металлов, их структуры и поведения в различных условиях.
Одним из основных аспектов изучения металлов в рамках математики является анализ их кристаллической структуры. Кристаллическая структура металлов определяется математическими моделями и методами, позволяющими описать упорядоченное расположение атомов или ионов в кристаллической решетке.
Важным разделом математики, связанным с изучением металлов, является статистическая физика и термодинамика. Эти разделы математики помогают объяснить физические явления, связанные с нагреванием, охлаждением и прочими процессами, происходящими с металлами при различных температурах и давлениях. С помощью математических моделей можно предсказать и объяснить изменения структуры и свойств металлов при изменении параметров окружающей среды.
Изучение металлов в рамках математики позволяет усовершенствовать производственные процессы, повышать качество и прочность металлических материалов, разрабатывать новые сплавы и материалы с оптимальными характеристиками. Также математические модели и методы позволяют более точно прогнозировать поведение металлов в экстремальных условиях и разрабатывать новые технологии и материалы для специфических областей применения.
Значение изучения металлов в курсе математики 11 класса

Изучение металлов является важной составляющей курса математики в 11 классе. Это связано со многими факторами и имеет реальное практическое применение в жизни. Знание свойств и характеристик металлов позволяет ученикам лучше осознавать математические модели и задачи, связанные с этой темой.
Во-первых, изучение металлов помогает понять и оценить реальные данные, которые широко используются в математике. Такие характеристики, как плотность, теплоемкость, электропроводность и температурный коэффициент, являются важными для многих математических моделей. При работе с такими моделями знание этих характеристик облегчает понимание задач и выбор подходящих математических методов для их решения.
Во-вторых, изучение металлов помогает развить аналитическое мышление. Анализ свойств металлов и их взаимосвязей требует внимания к деталям, логического мышления и умения рассуждать по моделям и зависимостям. Это помогает ученикам применять математические решения на практике и проследить логику рассуждений в реальных ситуациях.
В-третьих, изучение металлов способствует развитию навыков работы с данными и проведения анализа. Ученики изучают методы измерения и обработки данных, что позволяет преобразовывать эмпирические данные в числовые показатели и использовать их в математических моделях. Это также развивает умение работать с таблицами, графиками и диаграммами для визуализации и анализа данных.
Таким образом, изучение металлов в курсе математики 11 класса не только расширяет ученикам знания о различных материалах, но также развивает их аналитические и логические навыки, а также умение работать с данными. Важно не только понять математические модели, связанные с металлами, но и уметь применять эти знания на практике для решения реальных задач и ситуаций.
Основные свойства металлов в математике
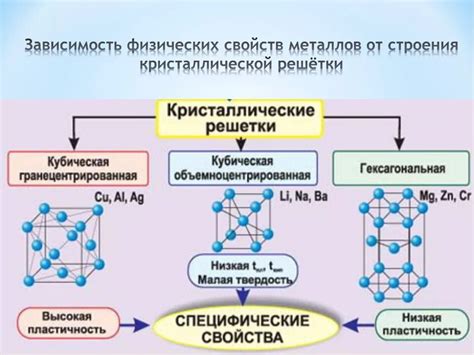
Металлы - это класс веществ, характеризующихся определенными свойствами, которые имеют большое значение в математике. Одним из основных свойств металлов является электропроводность. Благодаря свободным электронам в их структуре, металлы обладают способностью проводить электрический ток. Это свойство находит применение во многих математических моделях, где электропроводность является важным параметром.
Еще одно важное свойство металлов - теплопроводность. Металлы обладают высокой способностью передавать тепло, что также имеет большое значение в математике. Знание коэффициента теплопроводности металла позволяет моделировать и анализировать тепловые процессы, а также прогнозировать распределение температуры в различных системах.
Металлы также обладают высокой прочностью и пластичностью. Прочность металлов определяет их способность противостоять механическим нагрузкам, а пластичность позволяет им изменять свою форму без разрушения. Эти свойства металлов широко используются в математических моделях, связанных с механикой деформируемого твердого тела и расчетами прочности конструкций.
Другим важным свойством металлов является коррозионная стойкость. Некоторые металлы обладают высокой устойчивостью к окислительным средам и коррозии, что позволяет им сохранять свои физические и химические свойства в течение длительного времени. Это свойство находит применение в математических моделях, связанных с прогнозированием долговечности и стойкости материалов.
Структура атомов металлов и ее влияние на математику

Структура атомов металлов имеет определенное влияние на математику и особенности их химических свойств. Металлы, как и все элементы, состоят из атомов, которые имеют ядро и электроны.
Ядро атома металла содержит протоны и нейтроны. Протоны имеют положительный заряд, а нейтроны не имеют заряда. Около ядра вращаются электроны, которые имеют отрицательный заряд. Количество протонов и электронов в атоме металла обычно равно, что делает атом электрически нейтральным.
Однако структура атомов металлов имеет особенность - электроны располагаются не равномерно по энергетическим уровням, а образуют так называемую энергетическую оболочку. Количество электронов в оболочке может быть различным, и это влияет на свойства и химическую активность металла.
Изучение структуры атомов металлов позволяет математике разрабатывать модели, предсказывающие и объясняющие свойства металлов. Например, математические модели позволяют предсказывать температуру плавления или химическую активность металла на основе его атомной структуры и количества электронов на разных энергетических уровнях.
Также структура атомов металлов влияет на математику в контексте электропроводности. Из-за наличия свободных электронов, металлы имеют высокую электропроводность. Математические модели позволяют описывать электронное движение в металлах и предсказывать их электропроводность.
Вычислительные модели металлов в математике

Вычислительные модели металлов в математике представляют собой математические модели, разработанные для описания и анализа свойств металлических материалов. Эти модели обычно базируются на физических принципах и уравнениях, которые описывают поведение металлов в различных условиях.
Одна из наиболее распространенных вычислительных моделей металлов - модель конечных элементов. В этой модели металл разбивается на множество маленьких элементов, называемых конечными элементами. Каждый конечный элемент имеет определенные свойства и характеристики, которые описывают его поведение под действием различных нагрузок.
Другая вычислительная модель металлов - модель молекулярной динамики. В этой модели металл рассматривается как ансамбль взаимодействующих атомов или молекул. Каждая частица в модели обладает определенной массой, скоростью и силой взаимодействия с другими частицами. Такая модель позволяет исследовать поведение металлов на микроскопическом уровне.
Применение вычислительных моделей металлов в математике позволяет улучшить понимание и прогнозирование свойств металлических материалов. Это особенно важно для разработки новых металлов с определенными характеристиками, а также для оптимизации процессов обработки и использования металлов в различных отраслях промышленности.
Выводы и результаты, полученные с помощью вычислительных моделей металлов, могут быть использованы для разработки новых материалов, проектирования металлических конструкций, а также для оптимизации процессов металлообработки. Таким образом, математическое моделирование металлов играет важную роль в развитии современной науки и технологий.
Применение металлов в математических моделях

Металлы играют важную роль в математических моделях, позволяя нам представлять и анализировать различные физические, химические и технические процессы. Они используются для создания различных математических объектов, таких как графики, диаграммы и таблицы, которые помогают нам визуализировать и понять сложные математические концепции и взаимосвязи.
К примеру, металлические проводники используются для построения моделей электрических цепей. Это позволяет нам изучать законы Ома, Кирхгофа и другие основные принципы электротехники. Металлы также используются для создания моделей тепловых процессов, где они во многих случаях представляют теплопроводность материалов.
Один из примеров применения металлов в математических моделях - это создание моделей металлической решетки. Эти модели позволяют анализировать и понимать различные физические свойства металлических материалов, такие как их механическая прочность и пластичность.
Важно отметить, что металлические материалы обладают определенными свойствами, которые делают их особенно полезными для создания математических моделей. Они обладают высокой электропроводностью и теплопроводностью, что позволяет использовать их для создания эффективных моделей электрических и тепловых процессов.
Исследование тепловых свойств металлов математическими методами
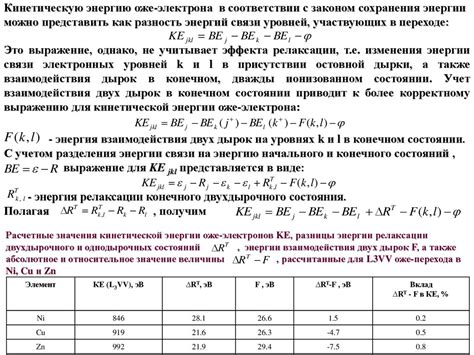
Тепловые свойства металлов являются важной характеристикой, которая может быть исследована с использованием математических методов. Одним из основных параметров, характеризующих тепловые свойства металлов, является коэффициент теплопроводности. Он определяет способность материала проводить тепло и зависит от его состава и структуры.
Для исследования теплопроводности металлов можно использовать математическую модель, которая описывает перенос тепла в материале. Эта модель основывается на уравнении теплопроводности и позволяет расчитать тепловой поток через материал и его температурное поле.
Используя математические методы, такие как численные методы или аналитические решения уравнения теплопроводности, можно определить коэффициент теплопроводности металла и его зависимость от различных факторов, таких как температура, структура материала или примеси. Такие исследования могут помочь в разработке новых материалов с улучшенными тепловыми свойствами или в оптимизации процессов нагрева и охлаждения металлических изделий.
Важным инструментом при исследовании тепловых свойств металлов с использованием математических методов является экспериментальная верификация результатов. Это позволяет проверить точность математической модели и использовать ее для предсказания тепловых свойств других материалов или условий.
Использование математических моделей для определения химических свойств металлов
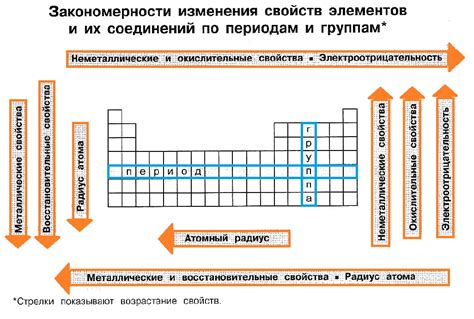
Математические модели активно используются в химии для определения химических свойств металлов. Эти модели позволяют установить зависимости между различными физико-химическими параметрами и предсказать поведение металлов под определенными условиями.
Одной из основных математических моделей, используемых для определения химических свойств металлов, является модель расчета энергии образования соединений. Эта модель позволяет предсказать, какие соединения металлов будут более или менее стабильными, и какие факторы могут влиять на их стабильность.
Другая математическая модель, используемая для определения химических свойств металлов, это модель расчета электронной структуры. С помощью этой модели можно определить, какие электронные уровни металла будут заполнены электронами, и какие металлы будут обладать высокой или низкой электропроводностью.
Математические модели также позволяют предсказывать свойства металлов при изменении температуры, давления и других условий. Например, с помощью этих моделей можно определить, какая будет температура плавления металла, его плотность, теплопроводность и теплоемкость.
Использование математических моделей для определения химических свойств металлов позволяет сэкономить время и ресурсы, которые были бы затрачены на проведение экспериментов. Кроме того, эти модели позволяют получать более точные и надежные результаты, что является важным фактором при проектировании новых материалов и разработке новых технологий.
Вопрос-ответ

Какие металлы изучаются в 11 классе при изучении математики?
В 11 классе при изучении математики изучаются различные металлы, такие как железо, алюминий, медь, свинец и золото.
Зачем изучать металлы в рамках изучения математики в 11 классе?
Изучение металлов в рамках изучения математики в 11 классе имеет несколько целей. Во-первых, это помогает понять принципы и основы математики на реальных примерах. Во-вторых, это позволяет изучать различные свойства и характеристики металлов, такие как плотность, прочность и теплопроводность. И, наконец, это помогает учащимся развивать логическое мышление и аналитические навыки.
