Металлы являются основой современной промышленности и широко используются в различных отраслях. Однако, чтобы использовать металлические материалы эффективно, необходимо проведение различных математических расчетов. Они помогают определить физические свойства металла, его прочность, устойчивость и другие параметры, которые необходимы для проектирования и производства изделий.
Основные методы математических расчетов по металлу включают в себя механику деформированного твердого тела, термодинамику и кинетику процессов, химическую кинетику и термодиффузию. Используя эти методы, инженеры и ученые могут предсказать поведение металла в различных ситуациях, оптимизировать процессы обработки и производства, а также создавать новые материалы с нужными свойствами.
Например, с помощью математических моделей и расчетов можно определить оптимальные параметры закалки металла, чтобы достичь необходимой прочности и твердости. Также можно провести анализ напряженно-деформированного состояния металлических изделий и предсказать их долговечность и надежность. Это особенно важно при разработке конструкций, которые будут подвергаться большим нагрузкам или в экстремальных условиях.
Математические расчеты по металлу широко применяются в различных отраслях, включая машиностроение, авиацию, строительство, энергетику и другие. Грамотное использование математических моделей позволяет повысить эффективность производства, снизить затраты на материалы и снизить риск возникновения аварийных ситуаций.
В заключение, математические расчеты по металлу являются неотъемлемой частью инженерной деятельности и позволяют оптимизировать процессы проектирования, производства и эксплуатации металлических изделий. На основе этих расчетов можно прогнозировать поведение металла, его прочность и устойчивость, а также создавать новые материалы с нужными свойствами.
Основные методы расчета металла
Математические расчеты по металлу выполняются с использованием различных методов, которые позволяют определить его свойства и произвести необходимые расчеты. Одним из основных методов является расчет механических свойств металла.
Этот метод позволяет определить прочность и устойчивость металла под воздействием различных нагрузок. Для этого проводятся испытания на разрыв, изгиб, сжатие и другие виды нагружения. Результаты этих испытаний позволяют определить предел прочности, упругость, пластичность и другие свойства металла.
Еще одним методом расчета металла является расчет коррозионной стойкости. На основе данных о составе металла и условиях его эксплуатации проводится оценка его устойчивости к коррозии. Этот метод позволяет определить толщину защитного слоя, необходимого для увеличения срока службы металла.
Также расчет металла может проводиться с использованием методов прогнозирования деформаций и трещин. При этом учитываются механические характеристики металла, условия нагружения и другие факторы, которые способствуют возникновению деформаций и трещин. Результаты расчета позволяют принять меры по предотвращению разрушения металла в процессе эксплуатации.
Метод конечных элементов: преимущества и недостатки

Метод конечных элементов – это численный метод, применяемый для решения различных инженерных задач, включая расчеты с использованием металлов. Этот метод основан на разбиении сложной геометрии объекта на малые элементы, называемые конечными элементами. Каждый элемент описывается математической моделью, которая позволяет рассчитать его поведение под действием внешних нагрузок.
Преимущества метода конечных элементов:
- Гибкость и универсальность. Метод конечных элементов может быть применен для моделирования и анализа различных физических явлений, включая статику и динамику, тепло- и массообмен, электромагнетизм и многое другое.
- Адаптивность. Метод позволяет уточнять результаты, добавляя или удаляя элементы, что особенно полезно при выполнении сложных расчетов.
- Учет нелинейных свойств материалов. Метод конечных элементов позволяет моделировать поведение материалов при деформациях, учитывая нелинейные эффекты.
Недостатки метода конечных элементов:
- Затратность. Расчеты с использованием метода конечных элементов требуют значительных вычислительных ресурсов, особенно при моделировании сложных систем.
- Необходимость проверки и калибровки модели. Метод конечных элементов требует тщательной проверки и калибровки математической модели, чтобы удостовериться в достоверности полученных результатов.
- Ограничения на форму и размер элементов. Метод ограничен использованием пространственных элементов, что может привести к неточностям при моделировании сложных геометрических форм.
При правильном применении и учете недостатков метода, метод конечных элементов является мощным инструментом для математических расчетов по металлу и находит широкое применение в инженерных расчетах и проектировании.
Метод конечных разностей: особенности применения

Метод конечных разностей является одним из наиболее эффективных методов для численного решения дифференциальных уравнений, учитывающих распределение физических величин в пространстве. Основная идея метода заключается в том, что вместо бесконечно малых приращений используются конечные разности, чтобы аппроксимировать производные и интегралы уравнений.
Одной из особенностей метода конечных разностей является его универсальность и применимость к широкому спектру задач. Он может использоваться для моделирования различных физических процессов, таких как теплопроводность, распространение звука, диффузия вещества и т.д. Кроме того, метод конечных разностей позволяет учесть различные граничные условия и неоднородности в системе, что делает его гибким инструментом для решения сложных задач.
Для применения метода конечных разностей необходимо провести дискретизацию области расчета, т.е. разделить ее на конечное количество узлов или ячеек. Затем на основе математической модели задачи, составляются разностные аналоги уравнений, учитывающие соответствующие разностные производные и интегралы. Полученная система уравнений решается численно, и на ее основе строится аппроксимация решения исходной задачи.
Плюсы метода конечных разностей включают его относительную простоту в реализации, возможность учета сложных геометрических форм и условий, а также возможность решения нелинейных уравнений. Однако, для достижения точных результатов, необходимо правильно выбрать шаг дискретизации и применять адекватные численные методы решения системы уравнений. Кроме того, метод конечных разностей требует значительных вычислительных ресурсов при работе с большими и сложными моделями.
Применение математических расчетов в металлургии
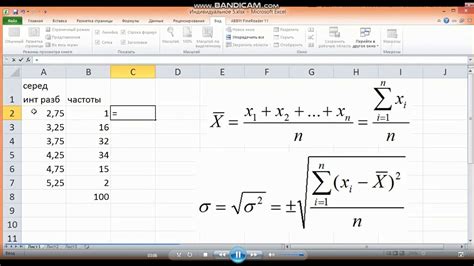
Металлургия – важная отрасль промышленности, занимающаяся изучением и обработкой металлов для производства различных изделий и конструкций. Для эффективной работы в этой сфере необходимо применение математических расчетов, которые являются неотъемлемой частью металлургического процесса.
Одной из основных областей применения математических расчетов в металлургии является проектирование и моделирование процессов обработки металлов. С помощью математических методов можно проанализировать физические и химические свойства металла, предсказать его поведение при различных условиях обработки и определить оптимальные параметры процесса.
Математические расчеты также применяются для определения механических свойств металлов. Используя решение уравнений и моделирование, можно предсказать прочность, пластичность и другие механические характеристики материала. Это позволяет инженерам и дизайнерам выбирать подходящий металл для каждого конкретного применения.
Еще одной областью применения математических расчетов в металлургии является разработка материалов с новыми свойствами. С помощью моделирования и оптимизации процессов можно создавать металлы с улучшенными характеристиками, такими как повышенная прочность или устойчивость к коррозии. Это позволяет снизить затраты на производство и улучшить качество конечных изделий.
Итак, математические расчеты играют важную роль в металлургии, помогая оптимизировать процессы обработки металлов, предсказывать их свойства и разрабатывать новые материалы. Без использования математических методов было бы гораздо сложнее достичь высокой эффективности в этой отрасли и решать сложные задачи. Поэтому знание и применение математических расчетов является необходимым навыком для специалистов, работающих в металлургии.
Расчет прочности металла при различных нагрузках

Расчет прочности металла является одной из ключевых задач при проектировании и изготовлении различных конструкций. Прочность металла определяется его способностью противостоять различным нагрузкам, таким как растяжение, сжатие, изгиб, скручивание и ударные нагрузки.
Проведение расчетов прочности металла позволяет определить, насколько надежным будет конструкция, противостоять тем силам, которым она будет подвергаться в течение своего эксплуатационного срока. В процессе расчета прочности учитываются множество факторов, таких как материал металла, его механические свойства, геометрические параметры конструкции и условия эксплуатации.
Для проведения расчета прочности металла при различных нагрузках используются различные методы, такие как аналитические расчеты, численные методы, методы конечных элементов и физическое моделирование. Каждый из этих методов имеет свои преимущества и недостатки, в зависимости от сложности задачи и требуемой точности расчета.
В аналитических расчетах применяются математические модели и уравнения, основанные на законах механики материалов. Преимущество таких расчетов состоит в их относительной простоте и возможности получения точного аналитического решения. Однако этот метод обладает некоторыми ограничениями и не всегда может учесть все физические и геометрические особенности конструкции.
Численные методы, такие как метод конечных элементов, являются более сложными, но более точными и универсальными. Они позволяют учесть сложные геометрические формы и неоднородности материала. При этом, наибольшую сложность представляет построение трехмерной модели конструкции и выбор правильных краевых условий.
Физическое моделирование включает создание физических макетов и их тестирование на различные нагрузки. Этот метод позволяет получить наиболее реалистичные результаты, так как учитывается влияние всех факторов, включая неоднородности материала и внешние условия. Однако данный метод требует больших финансовых и временных затрат, поскольку требует изготовления физических моделей и их испытания.
Прогнозирование деформаций металла при термической обработке
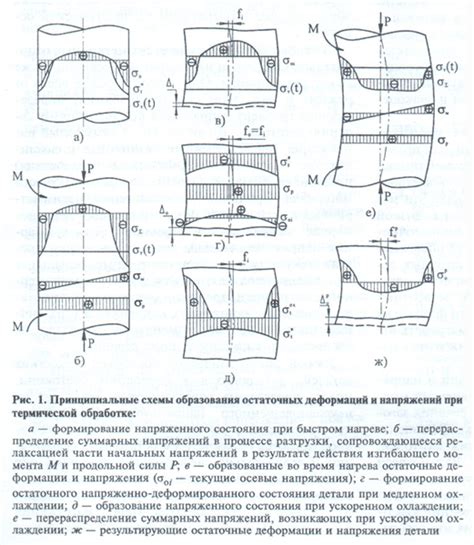
Для эффективного проектирования и производства изделий из металла необходимо учитывать деформации, которые возникают в результате термической обработки. Прогнозирование этих деформаций является важной задачей для инженеров и специалистов в области металлургии.
Одним из эффективных методов прогнозирования деформаций металла при термической обработке является использование численного моделирования. С помощью специализированного программного обеспечения можно создавать компьютерные модели и проводить виртуальные эксперименты, чтобы оценить потенциальные деформации.
При прогнозировании деформаций металла учитываются различные факторы, такие как свойства материала, температурный режим, внешнее воздействие и геометрические параметры изделия. Между этими факторами существуют сложные взаимосвязи, которые учитываются в численных моделях.
Прогнозирование деформаций металла позволяет оптимизировать процесс термической обработки и предотвратить нежелательные деформации. Это снижает количество брака и повышает качество готовой продукции. Также такой подход способствует сокращению времени и затрат на производство, что является важным фактором конкурентоспособности предприятия.
Вопрос-ответ

Какие методы использовать для математических расчетов по металлу?
Для математических расчетов по металлу можно использовать различные методы, в зависимости от конкретной задачи. Некоторые из наиболее эффективных методов включают метод конечных элементов, метод конечных разностей и метод конечных объемов.
В каких областях применяются математические расчеты по металлу?
Математические расчеты по металлу находят применение во многих областях. Они могут использоваться в инженерных расчетах при проектировании конструкций из металла, оценке прочности и деформаций, а также в анализе и оптимизации процессов обработки и изготовления металлических изделий. Кроме того, они могут использоваться для моделирования поведения металла при различных физических воздействиях, таких как тепло, напряжение или электрический ток.
Какие преимущества имеют математические расчеты по металлу?
Математические расчеты по металлу имеют ряд преимуществ. Они позволяют получить точные и качественные данные о поведении и свойствах металла, что позволяет снизить риск возникновения аварийных ситуаций и повысить надежность конструкций. Кроме того, такие расчеты позволяют сократить время и затраты на разработку и испытание новых изделий, а также оптимизировать процессы производства металлических изделий.
