Определение координат центра тяжести сечения швеллера является важным шагом в расчетах прочности и устойчивости конструкций. Швеллер – это прокатное изделие, представляющее собой двутавровую балку с геометрическими характеристиками, такими, как высота и ширина полок, толщина стенок и другие параметры.
Существуют различные методы для определения координат центра тяжести сечения швеллера, но самым точным и надежным способом является метод моментов. Он основан на равновесии моментов относительно оси, проходящей через центр тяжести сечения швеллера.
Для определения координат центра тяжести сечения швеллера методом моментов необходимо разделить сечение швеллера на элементарные площадки и вычислить их моменты относительно выбранной опорной оси. Затем необходимо сложить все моменты элементарных площадок и разделить их сумму на площадь сечения швеллера. Таким образом, получаем координаты центра тяжести сечения швеллера.
Использование метода моментов позволяет определить координаты центра тяжести сечения швеллера с высокой точностью, что является важным в решении задач прочности и устойчивости конструкций. Такой подход позволяет проводить точные расчеты и предсказывать поведение конструкции в действующих нагрузках.
Что такое швеллер и зачем он нужен

Швеллер – это тип профиля, который широко используется в строительстве и машиностроении. Он имеет форму буквы "Ш" и представляет собой две параллельные полки, соединенные поперечиной. Швеллеры выпускаются из стальных плит и имеют различные размеры и толщину.
Основная функция швеллера – это передача нагрузок в конструкциях. Он используется, как правило, в металлических конструкциях, таких как каркасы зданий, мосты, магистральные трубопроводы и т.д. Швеллеры обладают высокой прочностью и жесткостью, поэтому они способны выдерживать большие нагрузки.
Швеллеры широко используются и в производстве металлической мебели, лестниц, ограждений, других изделий различного назначения. Благодаря своей форме и конструкции, швеллеры обеспечивают устойчивость, надежность и долговечность конструкций. Благодаря возможности легко соединять швеллеры друг с другом, их можно использовать для создания сложных металлических конструкций различной формы и размеров.
Также, швеллеры могут использоваться для создания каркасов сэндвич-панелей, что позволяет создавать легкие и прочные конструкции с хорошей теплоизоляцией.
В заключении, швеллеры – это универсальный и незаменимый элемент металлических конструкций. Они обеспечивают прочность, устойчивость и долговечность, благодаря чему широко применяются в различных сферах промышленности и строительства.
Определение швеллера и его основные характеристики
Швеллер - это прокатный профиль, который используется в строительстве и машиностроении. Швеллер имеет форму буквы "С" с равнобедренными гранями и параллельными плоскостями. Он изготавливается из стали методом прокатки.
Швеллеры обладают рядом характеристик, которые определяют их применение и прочность. Одной из основных характеристик швеллера является его геометрическая форма, которая определяется размерами всего сечения и толщиной его стенок. Чаще всего швеллеры имеют прямоугольное сечение.
Координаты центра тяжести сечения швеллера также являются важной характеристикой. Центр тяжести - это точка, в которой можно представить массу швеллера сосредоточенной. Зная координаты центра тяжести, можно определить равновесие и силу, действующую на конструкцию.
Самый точный способ определить координаты центра тяжести сечения швеллера - это с использованием математических формул и интегралов. Однако, для обычных конструкций часто используются таблицы и специализированные программы для автоматического расчета центра тяжести.
Знание характеристик швеллера и его координат центра тяжести позволяет инженерам и архитекторам правильно расчитывать нагрузки и выбирать оптимальные конструктивные решения.
Как определить центр тяжести швеллера

Определение центра тяжести швеллера является одной из важных задач при проектировании и расчете конструкций. Центр тяжести швеллера представляет собой точку, через которую проходит результатирующая сила сечения. Зная координаты центра тяжести, можно рассчитать напряжения и деформации в конструкции и выбрать оптимальные параметры сечения.
Самый точный способ определить координаты центра тяжести сечения швеллера - это вычислить их аналитически с использованием геометрических данных о сечении. Для этого необходимо разделить сечение швеллера на элементарные фигуры с известными свойствами и вычислить центры тяжести каждой фигуры. Затем координаты центров тяжести фигур складываются с учетом их площадей и расположения, чтобы получить координаты центра тяжести всего сечения швеллера.
Определение центра тяжести швеллера также можно выполнить с использованием численных методов или сторонних программных средств, которые позволяют провести анализ геометрии и вычислить его координаты. Однако при использовании таких методов необходимо учитывать возможную погрешность расчетов и корректировать результаты при необходимости.
Методы и инструменты для точного измерения координат центра тяжести
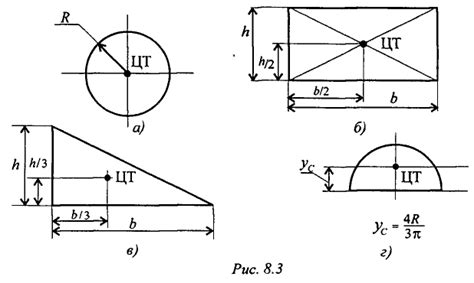
1. Графический метод. Один из наиболее простых и доступных способов определения координат центра тяжести сечения швеллера - использование графического метода.
Для этого необходимо построить прямоугольник, охватывающий сечение данной детали. Затем провести диагонали прямоугольника, пересечение которых указывает на координаты центра тяжести.
Этот метод достаточно быстрый и простой, но может давать неточные результаты при сложных формах сечения.
2. Механический способ. Для определения точных координат центра тяжести можно использовать механический способ.
Для этого нужно прикрепить швеллер к точке поворота и подвесить его на нити с разных сторон.
Затем, с помощью грузиков, уравновесить конструкцию таким образом, чтобы она находилась в горизонтальном положении.
Центр тяжести сечения швеллера будет находиться в точке пересечения нитей.
3. Математический анализ. Для получения более точных результатов можно применить метод математического анализа.
Этот метод основан на разбиении сечения швеллера на элементарные фигуры с простыми геометрическими формами (прямоугольники, треугольники и т.д.).
Затем для каждой элементарной фигуры необходимо вычислить ее площадь и координаты ее центра тяжести.
Далее производится суммирование этих значений с учетом взвешивания каждой элементарной фигуры и получаются точные координаты центра тяжести всего сечения швеллера.
4. Компьютерное моделирование. На современном этапе развития технологий широко применяются компьютерные методы и инструменты для определения координат центра тяжести сечения швеллера.
С помощью специализированных программ и программных средств можно построить трехмерную модель сечения швеллера и точно определить его центр тяжести.
Этот метод обладает высокой точностью и позволяет учесть сложную форму сечения и его материал.
Процесс определения координат центра тяжести
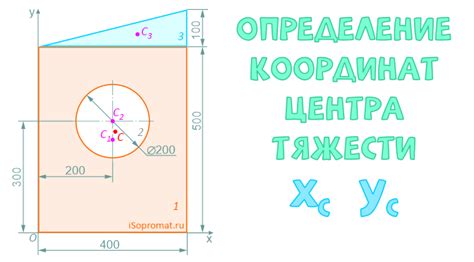
Определение координат центра тяжести сечения швеллера является важной задачей для точного расчета его характеристик и свойств. Для определения координат центра тяжести необходимо провести ряд последовательных вычислений и использовать базовые математические понятия.
В первую очередь необходимо разбить сечение швеллера на более простые геометрические формы, такие как прямоугольники, треугольники или полукруги. Затем необходимо найти площади каждой из этих форм, используя соответствующие формулы или методы расчета.
Далее следует определить расстояния от каждой из геометрических форм до выбранной оси координат, которую можно выбрать произвольно. Это позволит вычислить моменты каждой формы относительно этой оси. Моментом считается произведение площади формы на расстояние от нее до оси.
В итоге, для определения координат центра тяжести необходимо суммировать моменты каждой формы и поделить эту сумму на общую площадь сечения швеллера. Полученная координата является горизонтальным и вертикальным расстоянием от выбранной оси координат до центра тяжести.
Таким образом, процесс определения координат центра тяжести сечения швеллера требует разбиения сечения на простые формы, вычисления площадей и моментов каждой формы, а затем их суммирования и деления на общую площадь.
Шаги и подходы к определению координат центра тяжести
1. Определение геометрических параметров швеллера
Первым шагом в определении координат центра тяжести сечения швеллера является подсчет и измерение его геометрических параметров. Это включает в себя определение ширины, высоты, толщины и расстояний между различными элементами швеллера.
2. Разделение сечения на простые геометрические фигуры
Чтобы упростить расчет, сечение швеллера можно разделить на несколько простых геометрических фигур, таких как прямоугольники и треугольники. Это поможет в дальнейшем использовать известные формулы для определения центра тяжести каждой из фигур.
3. Расчет площадей каждой геометрической фигуры
После разделения сечения на простые фигуры необходимо вычислить площади каждой из них. Для прямоугольников это можно сделать, умножив длину на ширину, а для треугольников - используя специальные формулы, такие как половина произведения основания на высоту.
4. Определение координат центра тяжести для каждой фигуры
После расчета площадей каждой геометрической фигуры необходимо определить их координаты центра тяжести. Для прямоугольников это будет середина их высоты и ширины, а для треугольников - точка пересечения медиан.
5. Вычисление общей площади и координат центра тяжести сечения швеллера
Наконец, общая площадь сечения швеллера может быть вычислена путем сложения площадей всех простых фигур. Чтобы определить координаты центра тяжести всего сечения, можно использовать формулу момента, которая учитывает величины площадей каждой фигуры и их координаты центра тяжести.
Оценка точности полученных результатов
Определение координат центра тяжести сечения швеллера является важной задачей в инженерных и строительных расчетах. Однако, результаты этого определения могут быть в некоторой степени неточными из-за различных факторов.
Во-первых, точность определения координат центра тяжести зависит от точности измерений размеров и формы сечения швеллера. Малейшие ошибки в измерениях могут привести к значительным погрешностям в результате. Поэтому важно использовать точные и калиброванные инструменты для измерения размеров сечения.
Во-вторых, точность результатов может быть ограничена моделью, используемой для определения координат центра тяжести. Некоторые модели могут учитывать только простые геометрические формы, в то время как реальные сечения швеллера могут иметь более сложную форму или наличие отверстий и выступов. В таких случаях результаты определения могут быть приближенными.
Для повышения точности результатов рекомендуется проводить несколько независимых измерений и усреднять полученные значения. Также можно использовать более сложные математические модели, учитывающие особенности конкретного сечения швеллера.
Исходя из вышеизложенного, можно сделать вывод о том, что точность результатов определения координат центра тяжести сечения швеллера зависит от нескольких факторов, включая точность измерений, модель, применяемую для расчета, и особенности сечения. Поэтому важно применять все возможные методы для повышения точности результатов и учитывать возможность погрешностей.
Как проверить правильность определения координат центра тяжести

Определение координат центра тяжести сечения швеллера является важным этапом при проектировании конструкций и определении их прочностных характеристик. Ошибки при определении координат центра тяжести могут привести к неправильному расчету прочности и могут быть опасными.
Для проверки правильности определения координат центра тяжести рекомендуется использовать следующие методы:
- Геометрический метод: После определения координат центра тяжести сечения швеллера, можно визуально проверить правильность результата с помощью графического представления сечения. На графике необходимо отметить найденные координаты центра тяжести и убедиться, что они соответствуют расположению материала швеллера в сечении.
- Метод расчета моментов: Для проверки правильности определения координат центра тяжести, можно использовать метод расчета моментов с помощью главного момента инерции сечения. Найденные значения моментов должны совпадать с теми, которые были получены при определении координат центра тяжести, в противном случае требуется пересмотреть расчеты.
- Метод сравнения с известными значениями: Если для данного типа швеллера имеются известные значения координат центра тяжести, можно сравнить полученные результаты с этими значениями. Если найденные координаты совпадают с известными, это говорит о правильности определения координат центра тяжести. Если значения расходятся, необходимо провести дополнительные расчеты или проверить методику определения.
- Проведение экспериментов: Для окончательной проверки правильности определения координат центра тяжести можно провести физический эксперимент, например, с помощью весов и подвешивания швеллера поперек оси его центра тяжести. Результат эксперимента должен соответствовать найденным координатам центра тяжести.
Проверка правильности определения координат центра тяжести сечения швеллера является важным шагом, который необходимо выполнить перед применением полученных данных в дальнейшем проектировании и расчетах конструкций.
Практическое применение определения координат центра тяжести
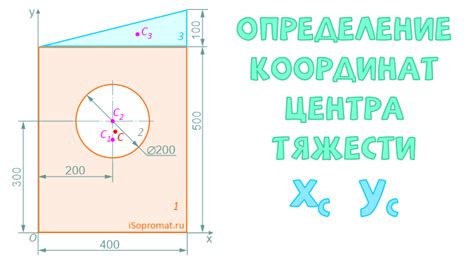
Определение координат центра тяжести сечения швеллера является важной задачей при проектировании и расчете конструкций. Знание точного положения центра тяжести позволяет определить распределение сил и моментов в швеллере, что в свою очередь позволяет предсказать его поведение при нагрузках.
Одной из основных применений определения центра тяжести является расчет реакций опор. Зная положение центра тяжести, можно определить моменты и силы, которые возникают в опорах при приложении нагрузок на швеллер. Это позволяет правильно распределить нагрузки между опорами и учесть их в дальнейшем проектировании.
Также определение координат центра тяжести имеет применение при расчете прочности конструкции. Знание точного положения центра тяжести позволяет определить точки, в которых возникают наибольшие напряжения и деформации. Это важно для выбора материала и формы швеллера, чтобы обеспечить необходимую прочность и устойчивость конструкции.
Другим практическим применением является определение момента инерции сечения швеллера. Момент инерции является мерой его сопротивления изгибу. Зная момент инерции и положение центра тяжести, можно определить напряжения и деформации, возникающие при изгибе швеллера. Это помогает предсказать его прочность и устойчивость при действии нагрузок.
Таким образом, знание и практическое применение определения координат центра тяжести сечения швеллера являются неотъемлемой частью проектирования и расчета конструкций. Они позволяют определить распределение сил и моментов, рассчитать реакции опор, выбрать подходящий материал и форму швеллера, а также предсказать прочность и устойчивость конструкции при действии нагрузок.
Примеры использования полученных данных в строительстве

1. Расчет несущей способности конструкции:
Знание координат центра тяжести сечения швеллера позволяет точно расчитать несущую способность его конструкции. Это особенно важно при проектировании и строительстве зданий и сооружений, где необходимо учитывать максимально возможные нагрузки, например, при возведении мостов, мачтовых конструкций или башен.
2. Определение точки приложения нагрузки:
Зная координаты центра тяжести сечения швеллера, можно определить точку приложения внешних нагрузок. Это важно при планировании расположения грузовых кранов, при выборе точки установки опор для подъемных механизмов и других грузоподъемных конструкций. Такой подход помогает обеспечить безопасность работ и оптимизировать использование грузоподъемного оборудования.
3. Расчет равновесия системы:
Координаты центра тяжести сечения швеллера необходимы для определения равновесия всей системы конструкций. Например, при строительстве больших зданий или сооружений, где важно обеспечить устойчивость и предотвратить возможность смещения или опрокидывания. Зная точные координаты центров тяжести всех конструкций, можно рассчитать и выбрать оптимальное расположение элементов, выдержать необходимые равновесию и грузоподъемности параметры.
4. Проектирование и создание новых конструкций:
Зная точные координаты центра тяжести сечения швеллера, можно использовать эти данные при разработке и создании новых конструкций различного назначения. Например, при разработке автомобильных кузовов, грузовых контейнеров или корпусов самолетов. Такие данные позволяют сделать конструкцию более эффективной, легкой и в то же время устойчивой и прочной.
Вопрос-ответ

Как определить координаты центра тяжести сечения швеллера?
Для определения координат центра тяжести сечения швеллера необходимо разделить сечение на элементарные фигуры, определить их площади и координаты их центров тяжести, а затем сложить все площади и координаты, поделив полученные значения на суммарную площадь.
Какой метод является самым точным для определения координат центра тяжести сечения швеллера?
Самым точным методом для определения координат центра тяжести сечения швеллера является метод разделения сечения на элементарные фигуры, нахождения их площадей и координат центров тяжести, а затем сложение всех площадей и координат с учетом их взаимного расположения.
