Определение положения центра тяжести швеллера является важным этапом в строительстве и проектировании металлоконструкций. Швеллер – это металлический профиль с формой буквы "С", используемый в качестве несущих элементов различных конструкций. Центр тяжести швеллера – это точка, в которой можно представить всю массу профиля. В соответствии с положением центра тяжести швеллера производится расчет нагрузок и определение сил в конструкции.
Для определения положения центра тяжести швеллера используется простая геометрическая формула. Во-первых, необходимо разделить профиль на несколько прямоугольников. Далее, для каждого прямоугольника найти его площадь и координаты его центра массы. Затем, найденные площади каждого прямоугольника умножаются на координаты их центров массы и складываются. В результате получается общая сумма, которую необходимо разделить на общую площадь профиля, чтобы получить координаты центра массы.
Зная положение центра тяжести швеллера, можно проводить дальнейшие расчеты и определение нагрузок, которые будут действовать на конструкцию. Это важно для обеспечения стабильности и надежности металлоконструкций, а также для оптимизации их проектирования.
Методы определения центра тяжести
1. Математический расчет
Один из наиболее точных методов определения положения центра тяжести швеллера - математический расчет. Для этого необходимо знать геометрические параметры швеллера, такие как высоту H, ширину B и толщину стенки t. С помощью формул и уравнений можно определить точное положение центра тяжести.
2. Графический метод
Другой метод определения центра тяжести - графический. Для этого на бумаге или компьютере строится схема швеллера в масштабе. Затем проводится разделение швеллера на малые элементы и определение их площадей. С помощью формулы центра масс можно вычислить положение центра тяжести.
3. Физический эксперимент
Третий способ определения центра тяжести - физический эксперимент. Для этого швеллер помещается на платформу с известными параметрами. Затем с помощью специального оборудования измеряются силы, действующие на швеллер, и их точные значения используются для определения центра тяжести.
4. Таблицы и справочники
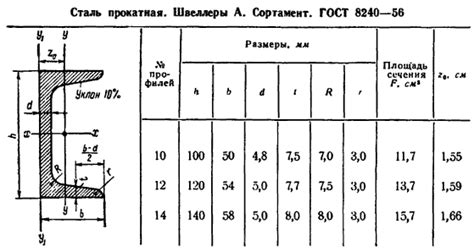
В инженерных расчетах можно использовать таблицы и справочники, где указаны геометрические параметры различных профилей, включая швеллеры. В таких таблицах указывается также положение центра тяжести для каждого профиля, что позволяет быстро и точно определить его положение.
5. Компьютерное моделирование
В настоящее время все больше инженеров используют компьютерное моделирование для определения положения центра тяжести. Методы конечных элементов и другие программные инструменты позволяют проводить точные расчеты, учитывая все особенности конструкции швеллера.
Определение центра тяжести швеллера в двух измерениях
Центр тяжести швеллера - это геометрическая точка, которая является аналогом центра массы данного конструкционного элемента. Определение положения центра тяжести швеллера в двух измерениях является важным для расчета его механических характеристик и статических нагрузок.
Для определения положения центра тяжести швеллера в двух измерениях необходимо знать геометрические параметры данного профиля. Основными параметрами являются высота швеллера, ширина полки, толщина полки и толщина стенки. Важно отметить, что все эти параметры должны быть выражены в одном едином измерении, например, в миллиметрах.
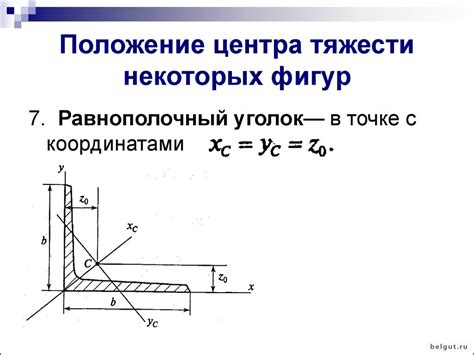
Существуют различные методы определения центра тяжести швеллера в двух измерениях. Один из наиболее распространенных методов - изобразительный. Для его применения необходимо построить схематичное изображение швеллера в масштабе, отметить геометрические параметры и провести линии, соединяющие середины сторон швеллера. Пересечение этих линий и будет являться центром тяжести швеллера в двух измерениях.
Также для определения центра тяжести швеллера в двух измерениях можно использовать математический метод. Для этого необходимо вычислить площадь каждой из частей профиля (полок и стенки) и их координаты центра тяжести. Затем, используя формулу момента инерции, вычислить положение центра тяжести для всего профиля швеллера.
В итоге, определение положения центра тяжести швеллера в двух измерениях является важным для решения различных инженерных задач. Знание этого параметра позволяет проводить расчеты механических характеристик и статических нагрузок швеллера, а также спроектировать надежные и устойчивые конструкции.
Определение центра тяжести швеллера в трех измерениях

Центр тяжести швеллера – это точка, в которой сосредоточена вся его масса и которая является показателем равномерного распределения веса по всей структуре. Определение положения центра тяжести швеллера в трех измерениях (по осям x,y,z) позволяет правильно распределить его при установке и расчете конструкций.
Для определения положения центра тяжести швеллера в трех измерениях, необходимо провести следующие шаги:
- Измерить геометрические параметры швеллера, такие как ширина, высота, и длина.
- Рассчитать площадь поперечного сечения швеллера и координаты его центра площади по осям x и y.
- Определить расстояние от центра площади до краев швеллера по осям x и y.
- Вычислить моменты инерции поперечного сечения швеллера относительно осей x и y.
- Рассчитать координаты центра тяжести швеллера относительно осей x и y по формулам.
- Определить положение центра тяжести швеллера по оси z, вычислив расстояние от нижней грани до центра тяжести поперечного сечения.
Таким образом, определение центра тяжести швеллера в трех измерениях является важным этапом при работе с этим типом конструкции, позволяющим обеспечить равномерное распределение веса и правильную установку.
Использование математических формул для определения центра тяжести
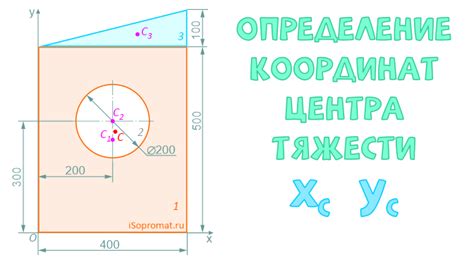
Центр тяжести швеллера - это точка, в которой можно считать сосредоточенной вся масса данной конструкции. Определение этого центра является важным шагом при проектировании и строительстве, поскольку это влияет на распределение нагрузок и стабильность конструкции.
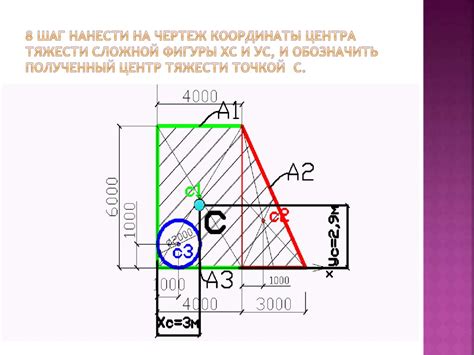
Определение центра тяжести швеллера возможно с использованием математических формул. Одним из методов является разделение швеллера на более простые геометрические фигуры, такие как прямоугольники и треугольники, и вычисление центра тяжести каждой из них.
Для расчета центра тяжести прямоугольной части швеллера можно использовать следующую формулу: x = (b*h^2/12)*(3c+h), где x - расстояние от точки, в которой находится центр тяжести прямоугольной части, до одного из боковых краев прямоугольника, b - ширина прямоугольника, h - высота прямоугольника, c - расстояние от центра прямоугольной части до бокового края.
Для расчета центра тяжести треугольной части швеллера можно использовать следующую формулу: x = (b*h^3/36)*((2lh)/(h/2+l)), где x - расстояние от точки, в которой находится центр тяжести треугольной части, до одного из боковых краев треугольника, b - ширина треугольника, h - высота треугольника, l - длина треугольника.
Далее необходимо учитывать площадь каждой части швеллера и их расстояние от некоторой базовой точки. После этого можно вычислить суммарный центр тяжести всех частей швеллера, используя формулу: x = (x1*A1 + x2*A2 + x3*A3 + ...)/A, где x1, x2, x3, ... - расстояния от базовой точки до центра тяжести каждой части швеллера, A1, A2, A3, ... - площади каждой части швеллера, A - суммарная площадь всех частей швеллера.
Примеры расчета центра тяжести швеллера
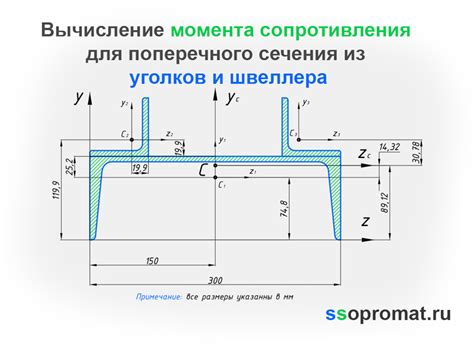
Пример 1:
Допустим, у нас есть швеллер с шириной полки b равной 100 мм, высотой полки h равной 150 мм, толщиной полки s равной 10 мм, толщиной стенки t равной 5 мм и длиной L равной 2000 мм. Чтобы найти положение центра тяжести, можно использовать следующую формулу:
x0 = (b * s2 + b * s * (h - s) + h * t * (h - t/2)) / (2 * (b * s + b * (h - s) + h * t))
Пример 2:
Предположим, что у нас есть швеллер с шириной полки b равной 80 мм, высотой полки h равной 200 мм, толщиной полки s равной 15 мм, толщиной стенки t равной 8 мм и длиной L равной 2500 мм. Для определения положения центра тяжести можно использовать данную формулу:
x0 = (b * s2 + b * s * (h - s) + h * t * (h - t/2)) / (2 * (b * s + b * (h - s) + h * t))
Пример 3:
Представим, что у нас есть швеллер с шириной полки b равной 120 мм, высотой полки h равной 180 мм, толщиной полки s равной 12 мм, толщиной стенки t равной 6 мм и длиной L равной 1500 мм. Для определения положения центра тяжести можно использовать следующую формулу:
x0 = (b * s2 + b * s * (h - s) + h * t * (h - t/2)) / (2 * (b * s + b * (h - s) + h * t))
Подставив значения в формулу, мы можем получить конкретное числовое значение для положения центра тяжести швеллера. Это значение поможет нам рассчитать необходимую поддержку и обеспечить правильное распределение веса при использовании швеллера в конструкции.
Области применения определения центра тяжести швеллера
Определение центра тяжести швеллера имеет широкое применение в инженерии и строительстве. Это понятие играет важную роль при проектировании и расчете конструкций из швеллера, таких как металлические балки или рамы.
Определение центра тяжести швеллера позволяет определить точку, где сосредоточена масса швеллера и где можно приложить силу, чтобы поддерживать его в равновесии. Это важно для расчета напряжений и деформаций в конструкции в процессе эксплуатации.
В строительстве определение центра тяжести швеллера используется при проектировании и монтаже металлических конструкций, таких как каркасы зданий, мосты, трубопроводы и т.д. Знание положения центра тяжести позволяет правильно распределить нагрузку и обеспечить стабильность и прочность конструкции.
Также, определение центра тяжести швеллера является важным при проведении расчетов статической и динамической устойчивости конструкций. Знание положения центра тяжести позволяет определить максимальные нагрузки, которые может выдержать конструкция без деформации или разрушения.
Кроме того, знание положения центра тяжести швеллера важно при транспортировке и подъеме металлических конструкций. Правильное расположение опорных точек и точки подъема позволяет безопасно перемещать и устанавливать тяжелые детали на строительной площадке.
Учет изменений в конструкции при определении центра тяжести
Определение положения центра тяжести швеллера является важным этапом расчета прочности и стабильности конструкции. Однако, при проектировании и строительстве могут возникать изменения, которые необходимо учесть при определении центра тяжести.
Внесение изменений в конструкцию, таких как добавление или удаление материала, изменение формы или размеров, может существенно повлиять на положение центра тяжести. При этом следует учитывать не только массу добавляемых или удаляемых элементов, но и их пространственное расположение относительно оси швеллера.
Для учета изменений в конструкции при определении центра тяжести следует использовать адекватные методы и инструменты. Один из наиболее распространенных способов - использование математических моделей и программного обеспечения для расчета центра тяжести при различных условиях.
Важно также иметь в виду, что изменения в конструкции могут привести к изменению динамических свойств системы. Например, перемещение центра тяжести может сказаться на ее устойчивости и возникновении дополнительных напряжений или деформаций. Поэтому, при внесении изменений необходимо тщательно проанализировать их влияние на центр тяжести и прочность конструкции в целом.
Вопрос-ответ

Как определить положение центра тяжести швеллера?
Чтобы определить положение центра тяжести швеллера, необходимо знать его геометрические размеры и плотность материала. Можно использовать формулу для расчета центра тяжести, которая основана на прямоугольной форме швеллера: x = b * h * (h/2) / (b * h), где x - расстояние от одного края швеллера до его центра тяжести, b - ширина швеллера, h - высота швеллера. Или можно воспользоваться табличными данными, где указаны координаты центра тяжести для различных типов швеллеров.
Как определить положение центра тяжести швеллера без использования формул?
Если вы не хотите или не можете использовать математические формулы для определения положения центра тяжести швеллера, можно воспользоваться графическим методом. Для этого нужно изобразить швеллер на бумаге в масштабе и провести ось симметрии. Затем, повесив швеллер на острие этой оси, находим точку равновесия - это и будет положением центра тяжести швеллера. Также можно воспользоваться специальными устройствами, например, весами, чтобы найти точку равновесия и определить положение центра тяжести.
