Площадь поперечного сечения металла является важным параметром, который необходимо учитывать при про
Основные методы расчета

Метод площадей - один из основных методов расчета площади поперечного сечения металла. В этом методе площадь поперечного сечения вычисляется путем разбиения его на простые геометрические фигуры, такие как прямоугольники или треугольники, и суммирования площадей этих фигур.
Метод интеграла - более точный метод расчета площади поперечного сечения металла. Он основан на использовании математического интеграла для определения площади под кривой, которая представляет форму поперечного сечения. Для этого метода необходимо задать уравнение кривой и вычислить интеграл по этому уравнению.
Метод конечных элементов - современный метод расчета площади поперечного сечения металла, основанный на численных моделях. В этом методе поперечное сечение разбивается на множество маленьких элементов, каждый из которых описывается математическими уравнениями и параметрами. Затем с помощью специальных программ проводится численное решение этих уравнений, позволяющее получить точную площадь поперечного сечения.
При выборе метода расчета площади поперечного сечения металла необходимо учитывать его сложность, точность, доступность программного обеспечения и доступность необходимых данных. Каждый из методов имеет свои преимущества и ограничения, поэтому важно выбрать наиболее подходящий метод в конкретной ситуации.
Методы нахождения площади поперечного сечения
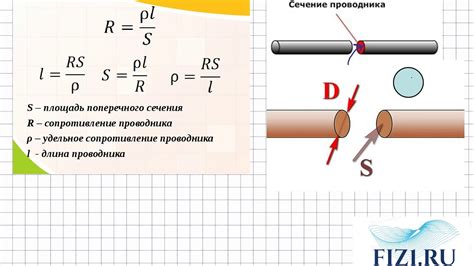
Для расчета площади поперечного сечения металла существует несколько методов. Один из них - метод геометрического измерения. Он основан на измерении размеров и формы сечения объекта. С помощью линейки, угольника, штангенциркуля, микрометра и других инструментов можно получить достаточно точные данные для расчета площади.
Второй метод - графический метод. Он предполагает построение графической модели поперечного сечения и вычисление площади с помощью геометрических формул. Например, если сечение имеет сложную форму, его можно разбить на простые геометрические фигуры, например, треугольники, прямоугольники, окружности, и затем вычислить площади каждой фигуры и сложить их.
Третий метод - математический метод. Он предполагает использование специальных формул для расчета площади. Например, для различных геометрических фигур, как прямоугольник, круг, эллипс, трапеция, существуют формулы для расчета площади без необходимости измерений. Этот метод позволяет быстро и точно расчитать площадь поперечного сечения без необходимости проведения измерений и построения графической модели.
Использование одного из этих методов зависит от сложности формы поперечного сечения и доступных данных. Иногда приходится применять комбинацию нескольких методов для достижения наибольшей точности в расчетах.
Формулы для расчета площади
1. Площадь прямоугольника
Для вычисления площади прямоугольника необходимо умножить длину стороны на ширину: S = a * b. Здесь S - площадь, а и b - длина и ширина соответственно.
2. Площадь квадрата
Площадь квадрата можно вычислить, умножив длину его стороны на саму себя: S = a * a. Здесь S - площадь, а - длина стороны.
3. Площадь круга
Формула для расчета площади круга связана с его радиусом и равна S = π * r^2. Здесь S - площадь, π - математическая константа (~3,14), r - радиус.
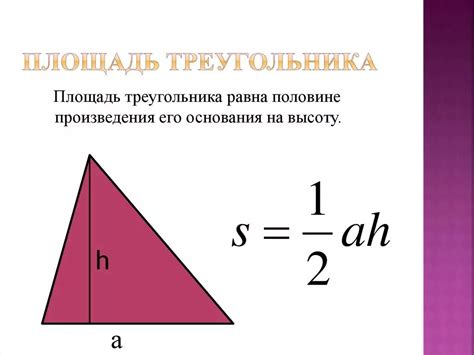
4. Площадь треугольника
Для вычисления площади треугольника можно использовать формулу Герона: S = √(p * (p - a) * (p - b) * (p - c)), где S - площадь, а, b, c - длины сторон треугольника, а p - полупериметр (p = (a + b + c) / 2).
5. Площадь трапеции
Площадь трапеции можно вычислить по формуле S = ((a + b) * h) / 2, где S - площадь, a и b - основания трапеции, h - высота.
Статические и динамические параметры
При расчете площади поперечного сечения металла необходимо учитывать статические и динамические параметры материала. Статические параметры включают в себя физические свойства материала, такие как плотность, упругость, теплопроводность и теплоемкость. Динамические параметры, в свою очередь, определяются механическим поведением материала при различных нагрузках.
Оценка статических параметров производится на основании данных из соответствующих таблиц и литературы. Значения плотности, упругости, теплопроводности и теплоемкости металла являются важными параметрами при расчете его площади поперечного сечения. Например, плотность металла влияет на его массу и грузоподъемность, а упругость определяет его способность сохранять форму под воздействием нагрузки.
Динамические параметры, такие как предел прочности, ударная вязкость и тепловое расширение, учитываются при расчете площади поперечного сечения металла, особенно при проектировании конструкций и механизмов. Предел прочности металла определяет максимальную нагрузку, которую материал может выдержать без разрушения. Ударная вязкость показывает способность материала поглощать энергию удара, а тепловое расширение определяет изменение размеров материала при изменении температуры.
Влияние статических параметров на площадь
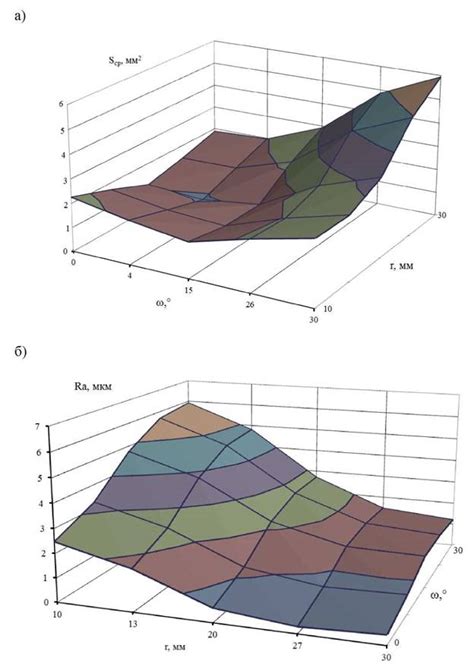
Площадь поперечного сечения металла является важным параметром, определяющим его прочность и устойчивость к различным нагрузкам. Несмотря на то, что формулы расчета площади могут быть достаточно сложными, статические параметры материала имеют значительное влияние на конечное значение данной величины.
Одним из основных статических параметров, влияющих на площадь поперечного сечения, является модуль упругости материала. Модуль упругости определяет способность материала сопротивляться деформациям при приложении нагрузки. Чем выше модуль упругости, тем меньше будет деформация и, следовательно, больше площадь поперечного сечения.
Еще одним статическим параметром, влияющим на площадь, является прочность материала. Прочность определяет предел допустимой нагрузки, которую может выдержать материал без разрушения. С увеличением прочности материала, его площадь поперечного сечения также может увеличиваться.
Если рассматривать площадь поперечного сечения металла в контексте конкретных конструкций, то важным параметром является геометрическая форма сечения. Различные формы сечений, такие как прямоугольные, круглые или треугольные, имеют различную площадь. Таким образом, выбор оптимальной формы сечения также может влиять на площадь материала.
В целом, статические параметры материала, такие как модуль упругости и прочность, а также геометрическая форма сечения, играют важную роль в расчете площади поперечного сечения металла. Правильный выбор и анализ этих параметров позволяет определить оптимальное значение площади и обеспечить требуемую прочность и устойчивость конструкции.
Влияние динамических параметров на площадь
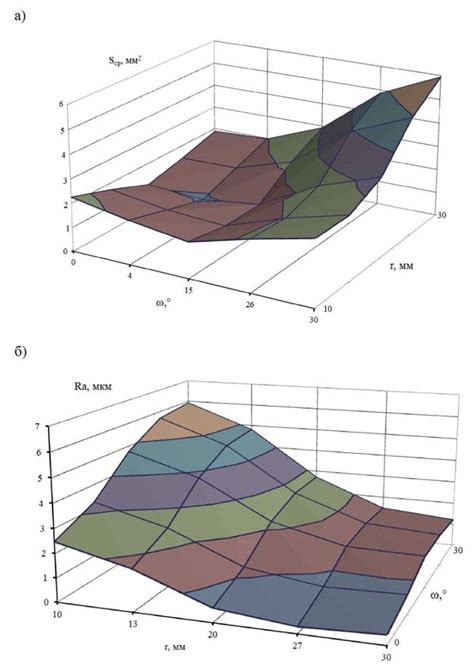
При расчете площади поперечного сечения металла необходимо учитывать влияние динамических параметров, так как они могут оказывать значительное влияние на итоговый результат.
Один из таких параметров - скорость деформации материала. Скорость деформации определяется как отношение изменения деформации к изменению времени. Увеличение скорости деформации может привести к увеличению площади поперечного сечения металла, так как это может стимулировать диффузию. В результате, металл может начать пластическое деформирование и увеличивать свою площадь.
Еще одним динамическим параметром, влияющим на площадь поперечного сечения металла, является температура. При повышении температуры металла происходит изменение его структуры и свойств. Это может привести к изменению площади поперечного сечения и его увеличению или уменьшению, в зависимости от типа материала и условий эксплуатации.
Также стоит отметить влияние скорости нагрева и охлаждения на площадь поперечного сечения металла. Скорость нагрева может вызвать расширение материала и увеличение его площади, а скорость охлаждения - сжатие и уменьшение площади. Поэтому при расчете площади необходимо учитывать эти параметры и проводить соответствующие корректировки.
В целом, для получения точного результата при расчете площади поперечного сечения металла необходимо учитывать все динамические параметры, такие как скорость деформации, температура, скорость нагрева и охлаждения. Это поможет предсказать изменения формы и размеров металла в различных условиях эксплуатации и принять соответствующие меры для обеспечения его надежности и безопасности.
Выбор оптимальных методов и формул

При расчете площади поперечного сечения металла необходимо выбрать оптимальные методы и формулы, которые позволяют получить точные и достоверные результаты. Важно учитывать особенности материала и его форму, а также требования конкретной задачи.
Один из самых распространенных методов - использование геометрических формул. Для простых и регулярных форм, таких как круг, квадрат или прямоугольник, можно применять стандартные формулы для расчета площади. Однако, для более сложных форм, например, для неправильных многоугольников или нестандартных фигур, требуется использовать более сложные методы.
Еще один метод - использование математических вычислений. Математические модели и алгоритмы позволяют получить точные значения площади поперечного сечения металла даже для сложных форм. Такие методы требуют глубоких знаний в области математики и программирования, но могут быть очень полезными при решении сложных задач.
Также можно использовать графические методы. Это включает визуальное измерение площади на графических изображениях поперечных сечений металла. Этот метод является достаточно простым и интуитивно понятным, хотя может не быть таким точным, как расчеты по формулам или математическим методам.
В конечном итоге, выбор методов и формул зависит от конкретной задачи и ресурсных возможностей. Важно учитывать точность результатов, сложность применения метода и доступность необходимых инструментов. Оптимальный подход - это использование комбинации различных методов для достижения наилучшего результата.
Особенности расчета площади поперечного сечения металла
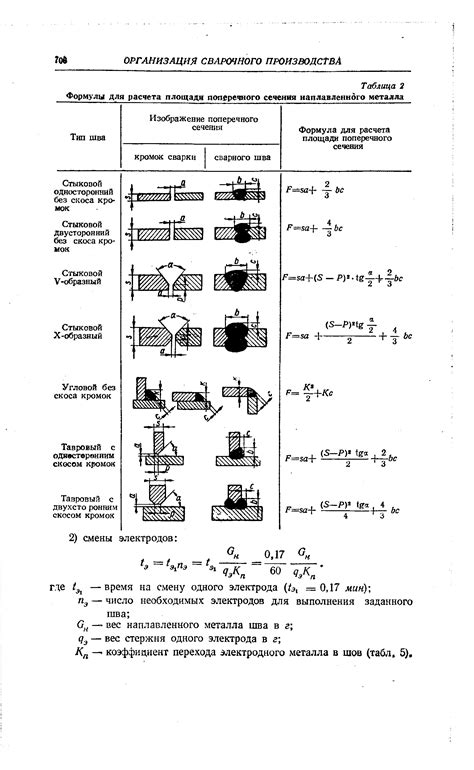
Площадь поперечного сечения металла является одним из важных параметров, используемых при расчете различных конструкций и деталей. Для определения этого значения необходимо учитывать ряд особенностей, которые связаны как с геометрическими характеристиками сечения, так и с особенностями материала.
Во-первых, при расчете поперечного сечения металла необходимо учитывать его форму. Существует несколько типичных форм сечений, таких как круглое, прямоугольное, квадратное и т. д. Каждая из этих форм имеет свои специфические характеристики, которые влияют на значение площади сечения.
Во-вторых, важно учитывать материал, из которого изготовлено поперечное сечение. Различные металлы имеют разные свойства, такие как прочность, термическая и электрическая проводимость и т. д. Эти свойства оказывают влияние на значение площади сечения металла.
При расчете площади поперечного сечения металла также необходимо учитывать возможность наличия отверстий или вырезов в сечении. Эти особенности могут существенно изменить форму и размеры сечения, поэтому необходимо учесть их при расчете площади.
В целом, расчет площади поперечного сечения металла является сложной задачей, требующей учета различных факторов. Точность и надежность расчетов напрямую зависят от правильного определения площади сечения, поэтому необходимо тщательно учитывать все особенности и параметры при расчете.
Вопрос-ответ

Какие методы используются для расчета площади поперечного сечения металла?
Существует несколько методов для расчета площади поперечного сечения металла. Один из самых распространенных методов - это метод подсчета геометрических фигур. Например, для прямоугольника площадь сечения можно вычислить как произведение его длины на ширину. Для сложных фигур, таких как окружность или эллипс, площадь сечения может быть рассчитана с использованием специальных формул.
Какая формула используется для расчета площади поперечного сечения прямоугольника?
Формула для расчета площади поперечного сечения прямоугольника очень проста. Она выглядит следующим образом: площадь = длина x ширина. Например, если прямоугольник имеет длину 5 метров и ширину 3 метра, то площадь его сечения будет равна 15 квадратных метров.
