Центр тяжести поперечного сечения швеллера – это геометрическая точка, которая является центром масс данной фигуры. Она определяется таким образом, чтобы сумма моментов относительно любой оси, проходящей через эту точку, была равна нулю. Определение центра тяжести является важным в задачах, связанных с расчетом прочности и устойчивости конструкций.
Расчет центра тяжести поперечного сечения швеллера осуществляется путем разделения поперечного сечения на элементарные площадки и определения их моментов относительно заданной оси. Затем производится суммирование моментов и нахождение координат центра тяжести. В результате расчета получается точка, в которой сосредоточено все массовое количество площадок, составляющих сечение швеллера.
Знание центра тяжести поперечного сечения швеллера позволяет проводить более точные расчеты прочности и устойчивости конструкций. В тех случаях, когда необходимо знать положение осей тяжести и моментов инерции относительно разных осей, определение центра тяжести является необходимой предварительной задачей.
Что такое центр тяжести поперечного сечения швеллера?
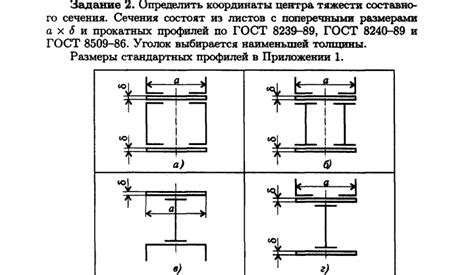
Центр тяжести поперечного сечения швеллера – это точка, в которой сосредоточена вся масса поперечного сечения. Точное определение центра тяжести является важной задачей при расчете и проектировании различных конструкций, таких как металлические фермы, рамы зданий, пролетные строения и другие.
Центр тяжести является ключевым параметром для определения распределения нагрузок и моментов в конструкции. Он позволяет определить точку приложения сосредоточенной силы, что обеспечивает баланс и стабильность системы.
Для швеллера, который является одним из наиболее распространенных элементов конструкций, определение центра тяжести поперечного сечения осуществляется путем вычисления суммарных моментов площадей элементарных частей швеллера относительно выбранного плоского сечения. Результатом расчета являются координаты центра тяжести по двум осям.
После определения координат центра тяжести поперечного сечения швеллера можно приступать к дальнейшим расчетам и проектированию конструкции, учитывая его положение и влияние на распределение нагрузок и моментов.
Определение и основные принципы расчета

Центр тяжести поперечного сечения швеллера – это точка, в которой можно сосредоточить всю массу сечения так, чтобы она не оказывала момента относительно оси, проходящей через эту точку. Определение центра тяжести является необходимым для проведения расчетов прочности швеллера.
Расчет центра тяжести поперечного сечения швеллера основан на базовых принципах теории механики. В основе расчета лежат следующие принципы:
- Принцип суперпозиции. При расчете центра тяжести поперечного сечения швеллера его можно представить как совокупность элементарных частей, каждая из которых имеет свою массу и свое положение. Таким образом, результирующие значения можно получить, сложив вклады всех элементов сечения.
- Принцип равенства моментов сил. Центр тяжести поперечного сечения швеллера находится на такой оси, где моменты сил относительно этой оси равны нулю. То есть, сумма произведений сил на их моменты относительно взятой оси равна нулю.
- Принцип равенства массы и мощности. Центр тяжести поперечного сечения швеллера располагается в точке, где сумма масс элементов сечения, умноженных на их расстояние от принятой оси, равна нулю. Таким образом, сумма масс элементов слева и справа от оси равна.
Расчет центра тяжести поперечного сечения швеллера проводится с использованием математических методов и формул. В результате расчета определяется положение центра тяжести относительно заданных координатных осей, что позволяет применять полученные значения при проектировании и анализе прочности швеллера.
Методы расчета центра тяжести
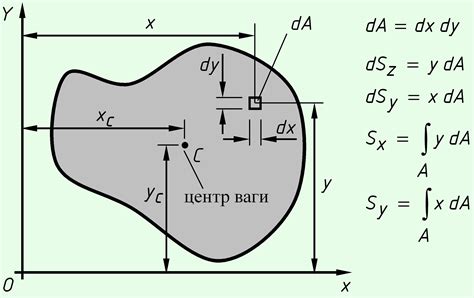
Определение и расчет центра тяжести поперечного сечения швеллера является важной задачей при проектировании и строительстве. Существует несколько методов, позволяющих определить положение центра тяжести швеллера с достаточной точностью.
Один из методов - метод графический. В данном методе сечение швеллера разбивается на элементы, для каждого из которых определяются его площадь и положение центра тяжести. Затем, путем графического построения, определяется положение центра тяжести всего поперечного сечения швеллера.
Другой метод - метод аналитический. В этом методе используется формула для определения центра тяжести поперечного сечения швеллера. Формула учитывает площади и координаты всех элементов, из которых состоит сечение швеллера. После подстановки всех значений в формулу, можно определить положение центра тяжести.
Также, для более сложных поперечных сечений швеллера может применяться метод численного расчета. В этом методе поперечное сечение разбивается на множество элементов, для каждого из которых вычисляется площадь и положение центра тяжести. Затем, через суммирование площадей и координат всех элементов, можно определить положение центра тяжести всего сечения швеллера.
Расчет момента инерции поперечного сечения
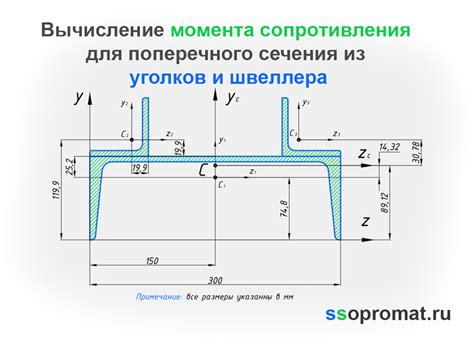
Момент инерции поперечного сечения является важным показателем, используемым при расчете прочности и устойчивости конструкций. Он определяет способность сечения сопротивляться изгибающим моментам. Момент инерции вычисляется относительно оси, которая проходит через центр тяжести сечения и перпендикулярна плоскости сечения.
Для швеллера расчет момента инерции выполняется на основе геометрических параметров сечения, таких как ширина полок (b), высота швеллера (h), толщина полок (t), толщина стенок (tw) и радиусы (r) округления внутренних и внешних углов сечения.
Формула для расчета момента инерции поперечного сечения швеллера может быть представлена как:
- Для простого швеллера (без отверстий):
- І = ((b * h^3) / 12) - 2 * ((tw * (h - t)^3) / 12)
- Для швеллера с отверстиями (при условии, что отверстия симметричны и расположены на одной линии):
- І = ((b * h^3) / 12) - 2 * ((tw * (h - t)^3) / 12) - n * (A * (y - (h/2))^2)
Где І - момент инерции, b - ширина полок, h - высота швеллера, t - толщина полок, tw - толщина стенок, r - радиус округления углов сечения, n - количество отверстий, A - площадь отверстия, y - расстояние между центром отверстия и осью симметрии швеллера.
Расчет момента инерции поперечного сечения швеллера позволяет определить его геометрические свойства, которые важны при проектировании и расчете конструкций из данного материала. Это позволяет обеспечить необходимую прочность и устойчивость конструкции при изгибе и других нагрузках.
Зависимость местоположения центра тяжести от формы сечения
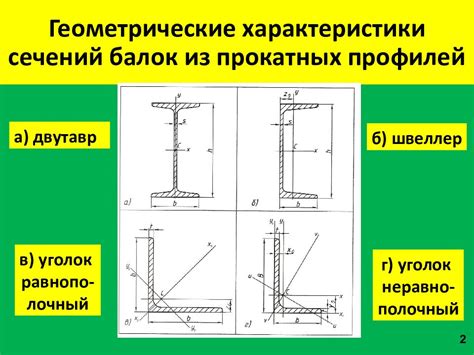
Местоположение центра тяжести поперечного сечения швеллера зависит от его формы. Центр тяжести - это точка, в которой сосредоточена вся масса сечения. А в случае швеллеров, местоположение этой точки влияет на его геометрические и механические свойства.
Форма сечения швеллера может быть различной: от прямоугольной до сложной, с использованием конических элементов. И каждая форма оказывает влияние на местоположение центра тяжести.
Например, если сечение швеллера имеет симметричную форму, то его центр тяжести располагается в центре сечения. Это делает его более устойчивым при нагрузке, так как сила распределена равномерно с обеих сторон от центра тяжести.
Однако, если сечение швеллера имеет несимметричную форму или присутствуют выступающие элементы, то местоположение центра тяжести смещается относительно центра сечения. Это может оказывать отрицательное влияние на его механические свойства и требовать дополнительных расчетов при проектировании конструкций.
В общем случае, центр тяжести поперечного сечения швеллера может быть определен с помощью математических методов или графическим способом. Знание точного местоположения центра тяжести важно при расчете напряжений и деформаций конструкции, а также при выборе оптимального типа швеллера для использования в конкретных условиях.
Примеры расчета центра тяжести поперечного сечения швеллера
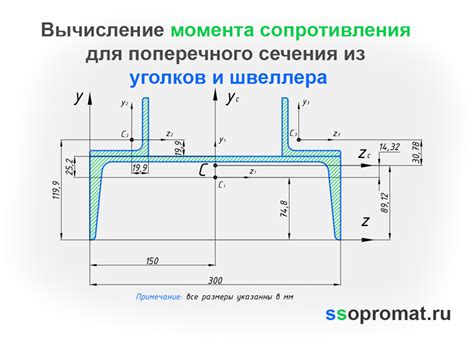
Расчет центра тяжести поперечного сечения швеллера является важной задачей для определения его механических свойств и прочности. Ниже приведены несколько примеров расчета центра тяжести для различных типов швеллеров.
Пример 1: Рассмотрим швеллер с поперечным сечением в форме прямоугольника. Чтобы найти центр тяжести данного сечения, необходимо знать его размеры. Предположим, что швеллер имеет ширину 100 мм и высоту 200 мм. Центр тяжести данного прямоугольного сечения будет находиться в середине относительно ширины и высоты, то есть в точке с координатами (50, 100).
Пример 2: Предположим, что швеллер имеет поперечное сечение в форме двух перевернутых треугольников, объединенных основанием. Высота каждого треугольника равна 150 мм, а ширина основания – 100 мм. Центр тяжести такого сечения можно определить, разделив его на два треугольника и находя центры тяжести для каждого из них. В данном случае центры тяжести обоих треугольников будут находиться на высоте 100 мм от основания.
Пример 3: В случае, когда поперечное сечение швеллера сложно и не может быть разделено на простые геометрические фигуры, центр тяжести можно найти методом численного интегрирования. Для этого необходимо разбить сечение на мелкие элементы и вычислить их моменты относительно выбранной оси. Затем суммировать эти моменты и разделить на сумму элементарных площадей, чтобы найти координаты центра тяжести.
Преимущества и недостатки различных типов сечений швеллера

Швеллеры — основной вид металлических профилей, применяемых в строительстве и машиностроении. Они обладают различными типами поперечных сечений, каждый из которых имеет свои преимущества и недостатки.
1. Полки одной ширины
Швеллеры с полками одинаковой ширины наиболее распространены из-за своей простоты производства. Они легко соединяются друг с другом и применяются в различных конструкциях. Однако у них невысокая гибкость в использовании в сложных пространственных конструкциях.
2. Полки разной ширины
Швеллеры с полками различной ширины обладают большей жесткостью и применяются в тех случаях, когда требуется высокая устойчивость конструкции. Кроме того, они обладают большим сопротивлением изгибу, что позволяет сократить количество используемых элементов. Тем не менее, процесс их производства более сложен и требует дополнительных операций.
- 3. Полки с учетом условий эксплуатации
Швеллеры с полками, учитывающими условия эксплуатации, обычно применяются в специальных конструкциях, например, в мостостроении. Эти швеллеры имеют нестандартные размеры и параметры, а также дополнительные элементы для обеспечения высокой прочности и устойчивости.
4. Невыпуклые полки
Швеллеры с невыпуклыми полками используются в тех случаях, когда необходимо снизить вес конструкции, например, при строительстве легких металлических конструкций. Они обладают высокой прочностью при низком весе и легко обрабатываются с помощью различных методов.
Каждый тип поперечного сечения швеллера имеет свои преимущества и недостатки, и его выбор зависит от конкретных условий и требований проекта. Необходимо учитывать такие факторы, как необходимая жесткость конструкции, требуемая прочность и устойчивость, а также особенности процесса производства и эксплуатации швеллера.
Применение расчета центра тяжести в строительстве
Расчет центра тяжести поперечного сечения швеллера является важной задачей в строительстве. Центр тяжести определяет точку, в которой предполагается, что вся масса объекта сосредоточена. Этот расчет позволяет определить равномерное распределение нагрузки на конструкцию и спланировать правильное размещение опорных элементов.
При проектировании и строительстве сооружений, таких как мосты, здания, металлические конструкции и т. д., очень важно знать точное положение центра тяжести. Использование расчетов центра тяжести позволяет инженерам обеспечить оптимальную стабильность и прочность объекта, а также рационально распределить нагрузку на конструкцию.
Определение центра тяжести основывается на геометрических и механических характеристиках поперечного сечения швеллера. Специальные программы расчета позволяют с высокой точностью определить координаты центра тяжести, что облегчает процесс проектирования и создания конструкции. Результаты расчетов центра тяжести используются для определения распределения нагрузки, позволяя подобрать оптимальные параметры конструкции.
Использование расчета центра тяжести является неотъемлемой частью процесса проектирования и строительства в строительной индустрии. Корректно определенный центр тяжести позволяет создать устойчивую и безопасную конструкцию, которая выдерживает все необходимые нагрузки. Это является гарантией надежности и долговечности сооружения.
Вопрос-ответ

Что такое центр тяжести поперечного сечения швеллера?
Центр тяжести поперечного сечения швеллера - это точка, через которую проходит суммарное воздействие всех сил, действующих на сечение швеллера.
Зачем нужно определять центр тяжести поперечного сечения швеллера?
Определение центра тяжести поперечного сечения швеллера необходимо для правильного расчета его прочностных характеристик. Зная положение центра тяжести, можно определить моменты инерции и радиусы инерции сечения, что позволяет производить прочностные расчеты конструкций, в которых используется швеллер.
Как определить центр тяжести поперечного сечения швеллера?
Центр тяжести поперечного сечения швеллера можно определить различными способами. Один из популярных методов - метод графический. Необходимо нанести сечение швеллера на графическую плоскость и провести две любые прямые, пересекающиеся в точке. Центр тяжести будет находиться в точке пересечения этих прямых.
Как производится расчет центра тяжести поперечного сечения швеллера?
Расчет центра тяжести поперечного сечения швеллера производится на основе геометрических параметров сечения. Необходимо знать координаты точек, из которых состоит сечение швеллера, а также их площади или массы. Затем, используя формулы математических центров, можно определить координаты центра тяжести сечения.
